The classical result of Sierpinski says that a compact connected Hausdorff space cannot be expressed as a countable union of nontrivial pairwise disjoint closed sets.

In this implies that a closed, bounded and connected subset cannot be decomposed in a countable union of nontrivial pairwise disjoint closed sets. A natural question arises: Can we construct a connected subset of a Euclidean space which decomposes into countably many pairwise disjoint closed sets? I stumbled a few days ago upon this this nice question.

Give this problem a try! For me it was a very nice exercise. I haven’t seen it in any textbook, which is quite suprising.

What follows is a short description of my first approach to the problem. This produces an example in instead of a plane (hence it deserves the name “ugly example”). Next, a differnet and much simpler example is introduced. I call it “Sun set”. Post finishes with historical remarks where the last example, Mullikin’s nautilus, is shown.

Ugly example

First, I’ve come up with an example in . Construction is fairly simple but wordy. Here are the pictures of it (third dimension, here depth, is only to make “bridges” to avoid intersections we see in the pictured 2D projection).

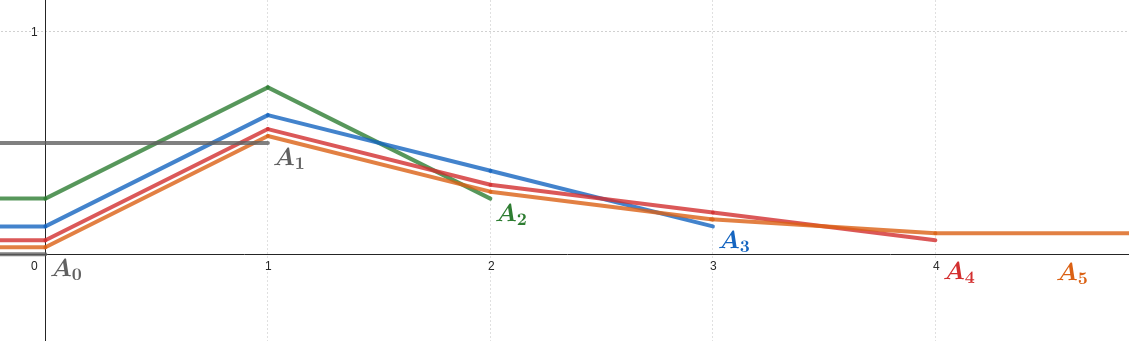
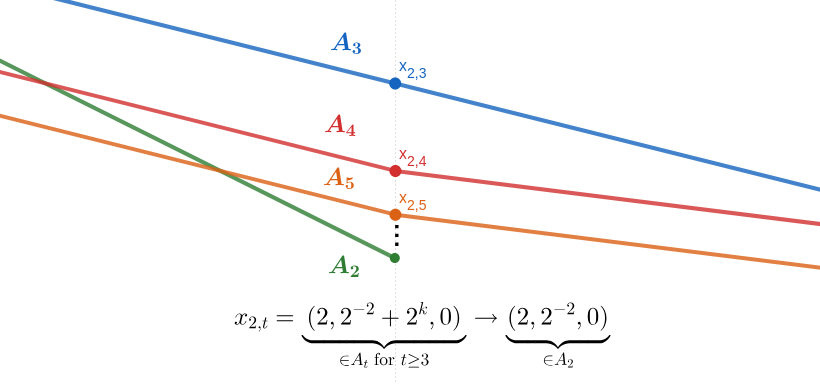
Here are the details of this construction, if you are interested in it.

I didn’t manage to simplify this construction so that it could live in the plane. It seems like the extra dimension for “bridges” to avoid crossings are necessary. This problem “fights” me, nice. A clever trick or a different approach is needed.

Sun set

I abandoned my original idea and went with a different approach. Here is a description of my example of a connected subset of a plane that can be written as a coutable union of nontrivial pairwise disjoint closed sets.

Let be a dense subset in the unit circle with . For each define the line segment And let . Finally, let . It clearly is a union of closed, pairwise disjoint, connected sets.

Theorem. is connected.

Proof. Let be open disjoint sets with . Without loss of generality assume that contains the origin . Since is connected, it must be contained in . It suffices to show that live in as well.

First, note that there is a natural number for which the ball is contained in the open set . Consequently, for each the endpoint of , namely , is close enough to the origin to be contained in . Hence, all with are in (since every is connected).

It remains to show that are also in the open set . Pick any index . By construction . Aiming for a contradiction, assume that lives in the open set . Then there is a neighborhood of with no points in common with . This is impossible because contains which is dense in the unit sphere. Hence belongs to , and so is in (’s are connected).

□

A historical note

Anna Mullikin, in her 1922 paper “Certain Theorems Relating to Plane Connected Point Sets”, constructs Mullikin’s nautilus. It is formed by taking a union of infinitely many polygonal chains. The first three are pictured below (screenshot from the original paper).

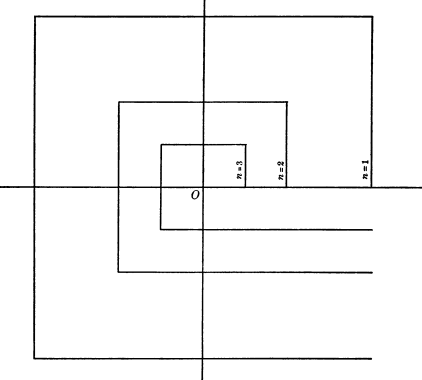
So neat! She has done something I couldn’t — her example has a similar feel to my first example in . But, with a clever shape, she obtained the needed limit points to “connect” parts without the necessity of my overengineered “3D bridges”.

The virtually same set was constructed by Kuratowski (see the second volume of his textbook titled “Topology”, or “Continuum theory” by Nadler). I thank my friend Julia who showed me this reference during math student conference OSSM 2024 in Kraków.

Post a comment if you come up with a different construction!