Εισαγωγή
Η αρμονική σειρά αποτελεί βασικό παράδειγμα στο οποίο η σειρά μιας μηδενικής ακολουθίας αποκλίνει. Αυτό οφείλεται στο γεγονός ότι η ακολουθία πάει αργά στο , κάτι που αναγκάζει την ακολουθία μερικών αθροισμάτων τής σειράς να αποκλίνει. Στο παρών άρθρο θα δείξουμε ότι η συμπεριφέρεται “τελικά” (δλδ για μεγάλα ) σαν λογάριθμος (άρα αποκλίνει, αλλά πολύ αργά).
Γεωμετρική απόδειξη
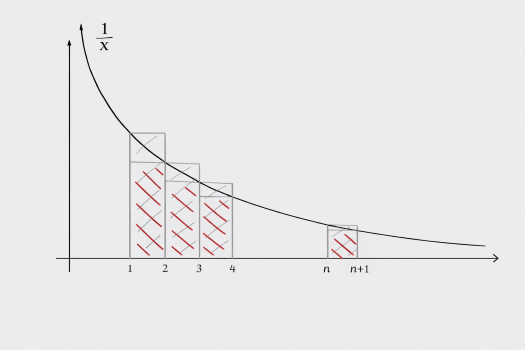
Παραπάνω βλέπουμε το γράφημα τής , . Κοιτώντας τα εμβαδά τών κόκκινων ορθογωνίων στο σχήμα παίρνουμε: ενώ από τα γκρί ορθογώνια παίρνουμε: δηλαδή
Συμπέρασμα
Η σχέση είναι αρκετή για να δείξουμε ότι , άρα , αφού , όπου . Ωστόσο, ο συνδυασμός των και , δηλαδή η σχέση , είναι που μας εξασφαλίζει ότι και λογάριθμος είναι “τελικά” συγκρίσιμες.
Σταθερά Euler-Mascheroni
Τώρα θα δώσουμε μια πιο λεπτή εκτίμηση, δείχνοντας ότι η απόσταση των ακολουθίων και συγκλίνει, άρα όντως τελικά οι δύο ακολουθίες είναι περίπου ίσες. Ορίζουμε την ακολουθία των αποστάσεων και αρκεί να δείξουμε ότι είναι ακολουθία Cauchy, άρα συγκλίνει. Από το προηγούμενο σχήμα είναι άμεσο ότι , άρα και για κάθε έχουμε
Τώρα, αφού καθώς , υπάρχει τ.ω. και αφού καθώς , υπάχει τ.ω. . Επομένως, για κάθε έχουμε
Το όριο τής παραδοσιακά συμβολίζεται με και είναι η λεγόμενη σταθερά Euler-Mascheroni.