Some Intuitive Concepts in Model Theory

Often times, logic can feel unintuitive and very syntactical, especially if you don’t spend a lot of time working with the ideas. This semester I’ve been doing a directed reading program in model theory, and I’ve found that model theory is actually the opposite! There are some very rich and intuitive concepts present in model theory, that I will try to describe here. My goal by the end of this blog post is to paint a picture of what exactly a model is, and what it means for a model to be atomic or saturated. It should be noted that the intended audience for this post is people who have some experience with propositional and first order logic. This is likely you if you have taken your school’s computer science discrete math class or intro to proofs class (or if you do any proof based math at all). Also, I am still learning this stuff, and this post is to help me understand it better, so if there is any incorrect concepts, please let me know!

Motivation

Often times I find the motivation behind many mathematical structures unmotivated, so here I will try to first motivate what a model is, using some anologies.

Syntax versus Semantics

The difference between syntax and semantics is a pervasive idea that shows up in everywhere from linguistics to theoretical CS. The best way to explain it is using natural language. In English, we have a grammar that describes how we should form sentences. It doesn’t tell us much about what that sentence means though. To demonstrate this, we can construct a sentence that is syntactically correct, but semantically meaningless. The canonical example in linguistics is “Colorless green ideas sleep furiously”. It is clearly grammatically correct, but it is not semantically meaningful, which seperates the notions. Another example, for programmers, is in Python there is a way to form valid programs (i.e. ones that parse), but this doesn’t say anything about what the program actually does.

Propositional Logic

Let’s first remember our propositional logic basics. As a very rough review, propositional logic is the logic where we have a set of variables, and then we have the logical connectors . Some example sentences in propositional logic are

We want to be able to reason about these sentences. What does it mean for a sentence to be a tautology? What about what does it mean for one sentence to entail another? These questions can be answered in two ways: syntactically, and semantically.

Syntax wise, this introduces the proof system we have all worked with. We have inference rules like modus ponens, proof by contradiction, disjunctive syllogism, etc. They tell us how to manipulate sentences to prove things. It is purely a syntax driven exercise: we don’t have to have any understanding of the meaning of these sentences to push them around. If we can start with a set of sentences , and prove some sentence , we write . We say that a sentence is consistent if there is no sentence in our language where .

Semantic wise, we use valuations: total functions from the set of variables in our language to the set . Given a valuation, , we define a model, , as a total function from the set of all possible sentences to the set . Before defining a model, I present some vocab. We then say a sentence(or a set of sentences) has a model/is satisfiable if and only if there exists a model where (or for a set of sentences, that makes every sentence true). We also say that given a set of sentences, , it models/satisfies a sentence if and only if for all models that satisfy , they also satisfy . This is written as . Finally, the obvious way to define models is as follows:

The natural first question to ask is, do these notions coincide? Is our syntax based transformations as strong (but not stronger!) than our semantic models? Thanks to the logicians of the past, we know that this is true. To put it formally, we say that a sentence is consistent if and only if it has a model. We can also use this notion to talk about sets of sentences. We say that a set of sentences, , is consistent if and only if it is satisfiable. Finally, we know that if and only if . This theorem is called the soundness and completeness theorem. I will not go into the proofs of these statements, but it is sufficient to internalize the idea that in our vanilla propositional logic, syntax crunching is the same notion as semantics.

First Order Logic

Now moving onto first order logic, we have a significant increase in degree of complexity. To review, for formulas in first order logic are “parameterized” by a language. What this means is that we fix a language, , which is a set of constant symbols, , a set of function symbols (each with an attatched arity) , and a set of relation symbols (also with an attatched arity) . We can then write formulas in our language. Something that should be noted is that shouldn’t be denoted as a formula! It doesn’t say anything. We call these types of expressions as terms. More formally, terms are just constants, function applications to terms, or variables. It should also be noted that in first order logic, formulas can have free variables, which are just variables that aren’t introduced using a quantifier. We write to signify that the free variables of are within (it doesn’t have to use all of them). Here are some examples of first order formulas.

We call a formula with no free variables a sentence.

Much like with propositional logic, I won’t go into the actual inference rules of our system, as I am assuming you are already familiar with these. I instead will go straight into defining models. We want a way to reason about our formulas in a semantic way much in the same way we reason about propositional calculus. We need some “environment” where we assign things values (like valuations did). We define this as a model. A model, , of a language, , is a non-empty set , called the universe, equipped with

Rather than go through the super dry and boring definition of what it means for a model to satisfy a formula, I would like to rather describe what it should mean, and go from there. First off, models have to fulfill formulas, which may have free variables. So, we should have some extra information: we say a model satisfies a formula at a tuple . Next, we should realize that terms should represent elements of , and the formulas that are operations on terms ( or relations) should be just checking if the property holds for the value in the term represents. To clear up this notion, let us take the example . We say that a model satisfies at if and only if in . Similarly, for terms, we say that our model satisfies the formula on if and only if is true in . Ok, so now, what should it mean for a model to satisfy the formula on . Well, it should mean that is satisfied on as normal, but whenever appears free in , we should be able to plug in any , and our model should satisfy it. Similarly, for , it means that there exists some that can be plugged into every free occurrence of , and our model would satisfy it. Notice that for sentences, we don’t need to write “on” anything, we can just say . Again, the syntax and semantics of first order logic have the same power. So, a sentence is consistent if and only if it has a model. Now that we have defined a model and how models and formulas interact, we can step back and realize that the world of models is very rich and large. To study models of a language, we traditionally take a set of sentences, , called a theory. We then study models of that theory (i.e. models that satisfy every sencence in ). We say a theory is complete if for every sentence , either or .

An example

The theory of a simple order, in the language with one 2-place relation (), is as follows (presentation from Chang and Keisler)

These sentences are also known as transitivity, antisymmetry, reflexivity, and comparability. We will call this theory from now on. An example of a model of this theory would be where here is the natural less than equal to realtion on the natural numbers.

Types

Let us say we have two different models in our language . They can be very different structures! From our previous example, take the model of our simple linear order from before. Also, take the model . These two models both satisfy our theory, . But, there is something very different about and . While has a least element, does not! For another example, look to the language with no relations symbols, two function symbols , and two constants . We can take two models of this language, and . Notice that is missing some elements that has: for example there is no element that satisfies the formula in , but there is one in . We want to be able to talk about the absence or presence of these objects in models, and so we will first formalize exactly what is the difference between these models. A type is a set of formulas with free. has to fulfills some specific properties for it to be a type, described below

The word maximal is new here. We say a set of formulas, is maximal if and only if for every formula , either or . Basically, if a set of formulas is maximal, that means it has made up its mind on what it wants any models to believe. There is nothing left to the imagination. Given some type , we say a model realizes it if there is some such that for every formula , our model satisfies on . We say a model omits So, an example of a type in is the set of all formulas, , that makes true about . This is obviously consistent (because the set has a model by definition) and is maximal (we take everything that holds true, so if something does not hold true, we add its negation). It is clear that realizes our type, while omits it, as some formula that looks like is in our type, and doesn’t have a least element. We want to be able to classify how rich or barebones a model is. Does it realize any type that it possibly could realize? Or does it realize only the types it has to realize? This brings in the two topics that this blog post is mainly about.

Atomic Models

Atomic models are the models that are bare bones. I will first provide the formal definition, then explore it through a topological space as a means for understanding it better. Fix some model of a complete theory . We say that a formula, , is complete with respect to if and only if for all in our language, exactly one of the following hold

where a theory models a formula if for every model of the theory, every element satisfies the formula. We then say that is atomic if and only if for all , there is some formula that is complete with respect to that realizes.

Ok that was dense. At surface level, one might think how does this even have anything to do with types, let alone communicate that a model is barebones? Let us create a space in which to explore what that definition means. Take the set to be the set of all types that are consistent with (i.e.  is satisfiable). We then define the topology using a basis. For every formula in our language, we let be a basic set. Notice that this fulfills the topology rules of a topology, since we can use to get the empty set, and to get all types (since types are maximally consistent). For some context, this space is a stone space (not important, I won’t talk about that here). We want to investigate the types that are isolated points in this space. A type, , is an isolated point if and only if is open in our space. Well, notice that this is true if and only if there is some formula such that it is not in any other type (since every open set is the arbitrary union of basic sets). We know that this formula is complete with respect to . This is because logically “carries” all the information in , which is maximal and complete! We also know that is consistent with , so some model satisfies , meaning that only exactly one of the two conditions for a formula to be complete holds. These types that can be represented by a single formula are called principal types.

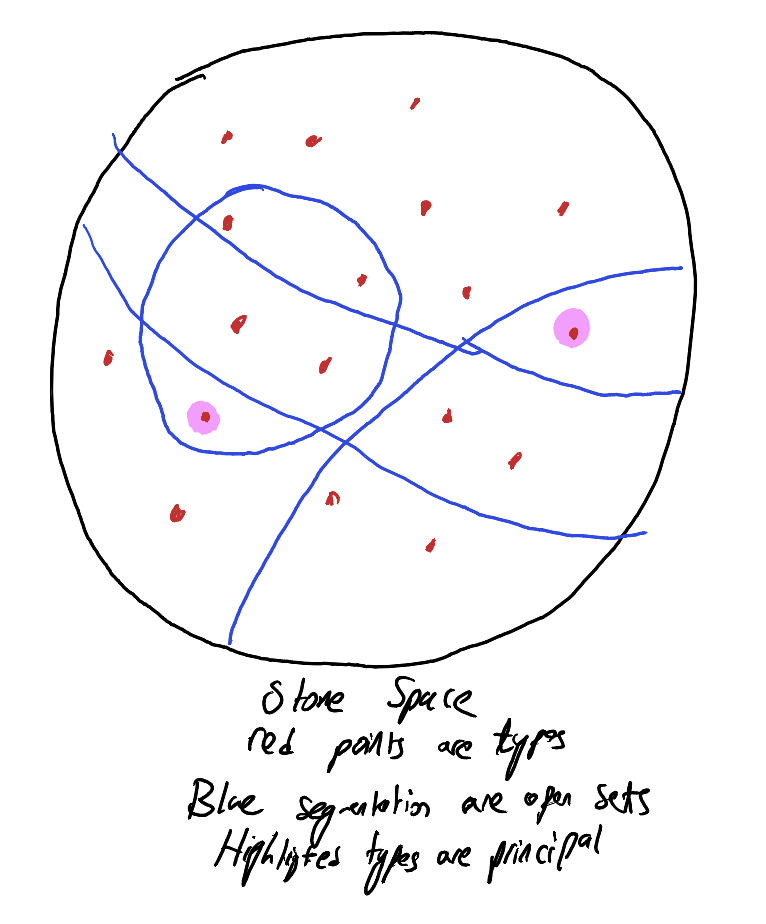
Ok, so we know that atomic models only realize principal types. How does this make them barebones? Well, take the sentence . We know that is complete, which means that either or . By soundness and completeness, we know that this is the same thing as saying or . We know that because is consistent with , so some model of exists where is realized. As such, , meaning every model of satisfies this type! By the definition of atomic, though, atomic models only satisfy these types. They only only satisfy the required, mandatory types that every model of satisfies! The “barebones” descriptor really makes sense now, doesn’t it.

Saturated models

Ok, so now that we talked about the minimalist models, we should talk about the maximalist models. These models contain everything they can possibly contain. Let’s try to workshop a definition for what this should represent. Fix some model of a complete theory . The first guess would probably be something like, “the model should realize every type that is consistent with ”. If you know any algebra, you probably can spot one reason why this notion could be strengthed though! Not all elements can be pinned down by just logical formulas. For example, the number or are not the solution to any polynomial (i.e. transcendental numbers cannot be expressed in the theory of fields). But, if we still want our model to be as rich as possible, it should be able to make create types that use these elements! To do this, we use a very common trick in model theory, that of expanding a model and a language. For any finite subset , we can expand our model to in the language as follows. Let (the language but we add a new fresh constant for every element ). For , we keep the model but just interpret every as . Now, we can effectively talk about the elements of in this language! Let be the set of all sentences true in an expanded model . We say that a model is saturated if and only if for every finite subset , every type in consistent with is realized in . Intuitively what this is saying is, give me any type (a list of requirements that we want our object to obey) that uses finitely many elements from our universe in a way that actually “makes sense” (it has to be consistent with ), and I will find an element in that realizes it. This communicates a “fullness” on a much higher scale than the previous definition we tried out. Now, for a model to be saturated, it has to contain types that even talk about elements in our universe that are not representable. This idea of extending a model and a language to include elements from our universe is a very common idea in model theory.

Examples

Ok, time for an example! It is actually the case that every complete theory has an atomic model and a saturated model. The following example is thanks to Andrzej Ehrenfeucht. Take the theory and language for a simple order, and add countably infinite many constant symbols. We then also add the following axioms to the theory of simple linear order, The first axiom adds density, the second axiom ensures there is more than one element, and the third and fourth axioms ensure there is no endpoints (i.e. no highest or lowest number). The fifth axiom is not actually an axiom, but rather an axiom schema. It is just telling us that we append the set to the theory. Take two different models

where we define and . Notice that tends towards infinity while tends towards . We will show that is atomic but not saturated, and is saturated but not atomic.

To see that is atomic, take any element . There are three cases. Assume for some . Then, the formula actually represents a principal type. This is because if , then there is no way there can be two different maximally consistent sets from this fact. Next, if , it is the case that represents a principal type. The way to intuitively think about this is that the elements below are indistinguishable. There is no formula that you can write that holds for some that doesn’t hold for . Similarly, if , then we know that there are is some such that . The formula also represents a principal type for the same reason as the last case. So, every element satisfies some principal type, meaning the model is atomic. The model is not saturated, though, as we can create a type for the “top” element that is not a principal type. Take to be the empty set (we don’t need to talk about any elements in to show it is not saturated), and take the set . is consistent with (using an appeal to the compactness theorem, which I have not outlined here so you will have to take my word for it). But obviously, is not a principal type. Since our model is atomic, then, there is no rational number satisfying this model

Notice that this model is not atomic. To see this, take some rational number . Then, the only formulas that realizes are of the form for some (or more complex formulas than this that are just conjunctions/disjunctions/negations of phrases like this). This formula isn’t complete though! Notice that doesn’t specify wether or . So, we are done. This model is saturated though! The reason for this is that since our sequence converges to an irrational number, there is no way to “tear” apart the elements above the sequence and the elements below. Imagine our sequence converged to a rational instead. Then, we could easily describe an element above all constants but below . But, because of the fact we cannot talk about and the density of in , there is no way to talk about the “top” of the sequence without having some element come after.

Conclusion

If that was messy I apologize, I didn’t really proof read this as it was more just a demo of this website (which I really like, it makes writing math on the web so easy). To recap, we have complete theories. These theories pin down everything that should be true and everything that should be false. We call two models elementarily equivalent if they make exactly the same formulas true, and models of complete theories are exactly that. But, there are still differences in models that are elementarily equivalent! They lie in the structure of the model, and how it satisfies types: does the model only have the mandated types required by the theory, or is the structure much richer and we have an element that captures every type. It should be noted that this presentation is a simplified version. In model theory, atomicity is not just for types over one variable, but instead for types over any finite amount of variables. Similarly, the notion of saturation presented here is what is called -saturation. There are stronger saturation conditions for other ordinals. Finally, if someone reads this and has any questions, finds something wrong, or has any suggestions, please comment. It seems that the ability of a comment section is a really good feature of this site. Oh, and also everything I’ve learned has been thanks to the textbook Model Theory by Chang and Keisler and my DRP mentor. Thanks for reading my post!