Chancy Grim Reaper Scenarios

The Classic Grim Reaper Paradox

: Fred is alive at For every positive integer and number of minutes elapsed since such that , there is a distinct Grim Reaper. This Reaper swings its scythe at Fred minutes past if and only if no Reaper does so earlier. (Henceforth I shall use “swing(s)” to mean “swing(s) its scythe,” except when I feel like writing the longer version. In the scenario at hand, the scythe may be assumed to be swung at Fred.) For any time between (exclusive) and (inclusive), Fred is alive at if and only if no Reaper swings earlier than

Suppose we count the Reapers from 1 onward, beginning with the Reaper poised to swing exactly one hour past The Reaper is the one poised to swing minutes past There are infinitely many Reapers poised to swing before the Reaper does.

There are only two possible cases, which I’ve named and . Either supposition leads to contradiction, as shown below.

: there exists a positive integer such that some Reaper swings minutes past

Let be one such positive integer .

The Reaper swings.
If the Reaper swings, then for no positive integer does the Reaper swing.
If for no positive integer does the Reaper swing, then the Reaper does and does not swing.
Therefore, the Reaper does and does not swing.

That the Reaper swings follows from and the definitions of and “the Reaper.” According to , there exists a positive integer such that some Reaper swings minutes past . But since is defined as one such positive integer (i.e., one such that some Reaper swings minutes past ), there must be a Reaper that swings minutes past . This Reaper can only be the one we call “the Reaper,” as this is by definition the only one poised to swing minutes past . Thus, the Reaper swings.

Premise 2 is a consequence of the stipulations of . Any given Reaper swings at Fred if and only if no Reaper swings at Fred earlier. Thus, the Reaper swings minutes past only if no Reaper swings less than minutes past . But for any positive integer , the Reaper is poised to swing less than minutes past . To see this, note that for any positive . So for positive , the duration minutes is less than minutes. Therefore, the Reaper swings only if the Reaper does not, for any positive integer .

I’ll give an example to illustrate the justification for premise 3. Let’s say . Then , which makes Reaper 2 the Reaper. So to establish premise 3, we need to argue that, without loss of generality:

3*. If for no positive integer does the Reaper swing, then Reaper 2 does and does not swing.

Now, from the supposition that the Reaper does not swing for any positive integer , it follows that neither Reaper 2 nor Reaper 3 nor any Reaper assigned an integer greater than 1 swings. Thus we see already that the second conjunct (“Reaper 2 does not swing”) of the consequent of 3* follows from the antecedent of 3*. What about the first conjunct, i.e., “Reaper 2 does swing”? As observed a moment ago, no Reaper assigned an integer greater than 1 swings, assuming the antecedent of 3* is true. Thus, neither does any Reaper assigned a number greater than 2 (e.g., Reaper 3, 4, or 5). But if no Reaper assigned a number greater than 2 swings, Reaper 2 does, for Reaper 2 swings if no Reaper swings before it does. So we get the contradictory result that Reaper 2 does, yet does not, swing.

The conclusion of the argument above follows from the premises by modus ponens/conditional proof. So we’ve shown that entails a contradiction. Next we derive a contradiction from .

: there exists no positive integer such that any Reaper swings minutes past

None of the Reapers swings.
If none swings, one does.
So, one of the Reapers swings.
Therefore, none of the Reapers swings, but one of the Reapers does.

, conjoined with , straightforwardly implies premise 1. By stipulation, for each Reaper there is some positive integer such that the Reaper swings minutes past , if the Reaper swings at all. If there exists no such for any Reaper, none of the Reapers swings.

But if none swings, then some Reaper (in fact, every Reaper) is such that none of the ones poised to swing before swings does so. So swings, for a Reaper swings as long as no Reaper has done so yet. This establishes premise 2.

We may apply modus ponens to infer 3 from 1 and 2. Then, to reach the desired contradictory conclusion, we simply conjoin 1 and 3.

The Unsatisfiable Pair Diagnosis

Causal finitists such as Rob Koons claim that the scenario is impossible because no infinite causal regress is possible. But Joe Schmid and Alex Malpass beg to differ. According to Schmid and Malpass’s unsatisfiable pair diagnosis (UPD) of infinitary paradoxes like , what makes these scenarios impossible is rather that each scenario requires two conditions to be met that cannot be met at once. Here’s one way to loosely characterize those conditions in the case of : i) there is an infinite causal regress, and ii) each cause in the regress is the (non-)occurrence of a distinct Grim Reaper’s swing, with the swing occurring if and only if (and because) none of the infinitely many earlier Reapers’ swings occurs. Given (i) and (ii) we run into the contradictions discussed above. But (i) entails no apparent contradiction on its own, so it’s plausibly possible despite the impossibility of certain infinite regresses.

In reply to the UPD (which Pruss calls “the Inconsistent Pair response” to the Grim Reaper paradox), Alex Pruss develops a new version of the Grim Reaper scenario, to which he believes no satisfactory Inconsistent Pair response can be given. It goes something like this:

: Fred is alive at Let for every integer . There exists some nonnegative integer such that

(a) for every integer , a distinct Grim Reaper swings its scythe at Fred minutes past if and only if Fred is alive then, and

(b) for any time between (exclusive) and minutes past (inclusive), Fred is alive at if and only if no Reaper’s swing before kills him.

The probability that the Reaper’s swing would kill Fred is , where is the same positive real number for every Reaper.

It is unclear whether Pruss intends for there to be a distinct Reaper for every positive integer, or merely one for every integer greater than some nonnegative integer But in either case, we can describe the situation by saying, as I have, that there’s a distinct Reaper for every integer greater than some nonnegative integer If there is a distinct Reaper for every positive integer, then Otherwise

I added stipulation (b) to avoid going down a rabbit trail. Without this stipulation, Fred may be alive at even though some Reaper kills him before Fred might have died earlier than and been resurrected by , such that he could be killed again. But that’s irrelevant in this dialectical context. We are exclusively interested in the paradox that might arise when we suppose a Reaper attempts to do something if and only if no Reaper has already succeeded in doing that thing. So, really, whether Fred is alive is of no significance to us. What matters is whether a Reaper previously caused him to die. For this reason, rather than stipulating (b) separately from (a), we could just replace “Fred is alive” with “no Reaper’s swing has already killed Fred” in (a).

If we modify the scenario, we can even ignore altogether whether any Reaper’s swing kills Fred. Let’s say there’s no one around for the Reapers to kill, but they’re all eager to swing their scythes anyway. Now suppose that, the greater the , the weaker the Reaper. More precisely, the probability is that the Reaper would succeed in swinging its scythe (i.e., manage to lift it and make a swinging motion with it). Suppose in addition that the Reaper swings if and only if no Reaper swings earlier. Then there may be a chance that roughly the same paradox we teased out of will arise.

But how? So far we haven’t even explicated how my first formulation of is paradoxical. So let’s do that. For the rest of this post, I’ll stick with that initial formulation.

We shall use the locution “Reaper non-fatally swings” to say that Reaper swings its scythe at Fred but fails to kill Fred thereby. To say that Reaper does not non-fatally swing is thus not to affirm that Reaper ’s swing kills Fred, but to deny that Reaper swings and kills Fred as a result. This denial is consistent with Reaper ’s refraining from swinging altogether. Let be some nonnegative integer such that (a) & (b). leads to contradiction on the following supposition.

: there exists no integer such that, for every integer , the Reaper non-fatally swings.

Let be an integer.

For some integer , the Reaper does not non-fatally swing.
If, for some integer , the Reaper does not non-fatally swing, then there exists an integer such that, for every integer , the Reaper non-fatally swings.
So, there exists an integer such that, for every integer , the Reaper non-fatally swings.
Therefore, there does and does not exist an integer such that, for every integer , the Reaper non-fatally swings.

entails that, for every integer , there exists some integer such that the Reaper does not non-fatally swing. Therefore, since by stipulation is an integer greater than , there is an integer such that Reaper does not non-fatally swing. Let be one such integer , so that Reaper does not non-fatally swing. Observe that, by definition, any Reaper that does not non-fatally swing either does not swing or kills Fred upon swinging. This means that the Reaper either does not swing or kills Fred upon swinging.

Suppose the Reaper does not swing. Then Fred must not be alive when the Reaper would have swung; otherwise, it would have swung! But if Fred is not alive when the Reaper would have swung, there exists an integer such that the Reaper fatally swings. Let be one such integer For every integer , the Reaper non-fatally swings. So, there exists an integer —namely —such that, for every integer , the Reaper non-fatally swings.

Suppose instead that the Reaper kills Fred upon swinging at time . In that case, Fred must be alive at . But if he’s still alive then, every Reaper that swings earlier than non-fatally swings. In other words, for every integer , Reaper non-fatally swings. Recall that .

So, no matter what, there exists an integer such that, for every integer , the Reaper non-fatally swings. This directly contradicts , according to which no such exists. So, just as planned, we’ve deduced a contradiction.

Pruss’s Objection to the UPD

Notice that we only get that last contradiction by assuming is true. This is the crucial difference between and ; the latter scenario gives rise to a contradiction no matter what. In it’s logically possible to avoid paradox, since a Reaper is not guaranteed to kill Fred just as long as it swings its scythe at him. So in , some ways of filling in the details give us a possible situation; others don’t—the ones that generate contradictions. Taking into consideration this feature of the thought experiment, Pruss tries to back the proponent of the UPD into a corner by showing they’re committed to an inexplicable modal discontinuity. In particular, he suggests, though not as explicitly as he might’ve, that the only available Inconsistent Pair response to entails is impossible if but possible if . Let’s see if he’s right. (You may rightly be curious what he finds counterintuitive about this entailment and whether that intuition of his should be trusted, but that’s a discussion for another time.)

His central argument is this. Paradox, i.e., contradiction, can only be avoided in if is false. Consequently, is necessarily true, which makes it likely. But, at the same time, if , the probability of is zero. Thus, owing to the inconsistency and concomitant impossibility of a necessary event’s being both likely and likely, is impossible if . But since the probability of needn’t be (or is not) zero if , the UPD proponent should hold that remains possible if , due to its consistency in that case.

The thought is that is necessary because cannot be true without contradiction, and contradictions cannot be true; this is the sense in which “we have to avoid paradox,” to borrow Pruss’s phrasing. Naturally we might think that whatever is necessary, i.e., whatever cannot fail to obtain, is likely. For if it were less than likely, there would be some chance, and thus some possibility, of its failing to obtain. But nothing necessary possibly fails to obtain.

That much is straightforward. But why does Pruss think has a probability of zero in the event that ? Here’s why.

Recall that put simply, is the proposition that there is no Reaper, , such that all Reapers poised to attack Fred before try and fail to kill him. We’ll say those Reapers are “earlier than” . So , the negation of , is the proposition that all (the infinitely many) Reapers earlier than some Reaper non-fatally swing. To determine the probability of , we need to consider the probability of the failure of each member of an infinite subseries of the series of Reapers.

While presenting his Unreliable Reaper scenario, Pruss tells us that “[t]he probability that the Reaper’s swing would succeed in killing Fred is .” It may appear that only one event is involved, but in fact two are. There’s the event of the Reaper’s trying to kill Fred by swinging its scythe at him, as well as the event of the Reaper’s swing’s killing Fred, i.e., succeeding. Thus, “[t]he probability that the Reaper’s swing would succeed in killing Fred” is ambiguous, considered in isolation. It may mean the unconditional probability of the conjunction , or it may mean the probability of conditional on . Thus, is either a) the chance that the Reaper swings its scythe and thereby kills Fred or b) the chance, given that the Reaper swings at Fred, that this attempt to kill Fred succeeds.

The latter is perhaps the most charitable reading of Pruss. Had he meant the former, we would run into contradictions of a kind Pruss altogether neglects to mention. If you’re curious what contradictions those are and how they would undermine Pruss’s critique of the UPD, see Appendix A.

There are countably infinitely many Reapers you might single out for consideration. No matter which Reaper you choose, infinitely many Reapers are poised to attack Fred before that one does. And each of those earlier Reapers has a chance of killing Fred, given that it tries to kill him. For this reason, no matter which Reaper, , you choose, the probability is zero that all Reapers earlier than try and fail to kill Fred, supposing all Reapers (even those after ) try. Moreoever, as Pruss points out in a parenthetical remark, the union of countably many—even countably infinitely many—zero-probability events itself has probability zero. We have such a union here. For each of the countably infinitely many Reapers, there’s a distinct hypothetical event of the failure of all Reapers earlier than that one, representable as the intersection, or conjunction, of all the individual failures. We can take the union of all those zero-probability events, which represents their disjunction. That union, having countably many members, must itself have probability zero, conditional on all the Reapers’ swinging. That is, there’s zero chance that no Reaper kills Fred, assuming absolutely every Reaper in the series swings. Fred’s being killed by no Reaper has a conditional probability of zero—the condition being that every single Reaper swings. Whether it has an unconditional probability of zero is another matter, to be addressed shortly. At any rate, if you’re unconvinced of the probabilistic claims made thus far (and you probably shouldn’t be convinced), see Appendix B.

There needn’t be any tension between an event’s being necessary and its having a conditional probability of zero. For even if every necessary event must have an unconditional probability of one, a necessary event may have a conditional probability of zero, relative to certain conditions. Any event , be it necessary or contingent, has a probability of zero conditional on ’s nonoccurrence, denoted , or conditional on a conjunction (intersection) including as a conjunct. Moreover, the event of, say, Pruss’s posting the thought experiment on his blog in April of 2025 (though contingent) has in some sense an unconditional probability of one now that it has occurred, but it has a probability of zero on the supposition that Pruss has yet to post on his blog. The supposition is obviously false, but that doesn’t mean we can’t assign a probability based on that assumption. To do so is just to ask how likely it would be, in some hypothetical universe (where July comes after April as it does in our universe), for Pruss to post the scenario in April of 2025 if he had yet to post it by July of the same year in .

The general point of the previous paragraph seems to bear scrutiny, but it’s doubtful that it applies to the case at hand. The event whose probability is in question is that, for some , all Reapers after Reaper (henceforth “Reapers onward”) swing non-fatally. Arguably, if this particular event has a probability of zero conditional on Reapers onward’s swinging for some , it must also have an unconditional probability of zero. For this event partly consists in the condition that, for some , Reapers onward swing; that is to say, the event includes the condition relative to which we’re assigning the event a probability. Thus, whatever it is about the condition that makes the event likely, that is an intrinsic feature of this latter event, which makes it likely independently of conditionalization.

There’s another worry for Pruss’s argument though. It’s not actually necessary that there be some such that Reapers onward swing non-fatally. Thus, there’s no need to explain how there being such a is necessary despite being likely. Here’s a way to see that this zero-probability event needn’t be necessary. Note two distinctions: a) that between avoiding paradox in a Grim Reaper scenario and avoiding paradox, and b) that between an event’s being necessary and some condition’s necessitating it. What is commonly believed is that, necessarily, no contradiction is true. That is the sense in which we ostensibly must avoid paradox; we don’t need to narrowly avoid paradox, as we would were a situation like to arise without leading to some contradiction that could easily result. It’s possible for no such situation to arise in the first place. If none did, we could avoid paradox despite the nonoccurrence of the zero-probability event that Reapers onward swing non-fatally. We also know that, necessarily, if the story is true (and paradox avoidance is necessary), then there is some such that Reapers onward fail. In other words, it’s impossible for these two things to be true at once: 1) there’s no such , and 2) the scenario actually happens. For short we say (2) “necessitates” the negation of (1) (as does (1) the negation of (2)). It does not follow from this that it’s necessary simpliciter that there be some such that Reapers onward fail.

Why do I say there being such a is not necessary, rather than suspending judgment on whether it is? I say so because there are a plethora of possible situations where no such exists. Granted, if any of these possibilities is actualized, the story is false. But regardless of whether that story is true, these alternate scenarios are possible, and thus they may have nonzero probability.

One alternate possibility is that there are no Reapers. That’s not only possible; it’s reality! This is an alternate possibility because, if there are no Reapers, there are no Reapers onward that fail for any Another possibility is that none of the Reapers swings. But if none swings, none swings non-fatally. So none fails, i.e., makes an unsuccessful attempt to kill Fred. And if none fails, there’s no such that Reapers onward fail. It’s even conceivable that all the Reapers succeed, insofar as it’s conceivable that Fred is resurrected each time a Reaper kills him.

Therefore, even if , no zero-probability event need be necessary. And if none is necessary, we may infer from any event’s having probability zero that it does not have probability one (as it plausibly would were it necessary). So the story is not rendered impossible when we include in that story the supposition that As long as there’s no other inconsistent pair in , and I see no reason to think there is, those who accept the unsatisfiable pair diagnosis should be open to the idea that is possible even if

Appendix A

On the modest assumption that for some Reaper (that is, that there’s a Reaper 1), it follows that, for that Reaper, for any . But then there’s a chance that Reaper 1 kills Fred. Observe as well that there’s a chance of Reaper 2’s killing Fred, and that for any positive real . But as long as the probability of Reaper 1’s killing Fred and that of Reaper 2’s killing Fred are both nonzero and the two events are mutually exclusive, the probability that one or the other kills Fred is greater than the probability that Reaper 1 does, and greater than the probability that Reaper 2 does. We’ve seen that these two probabilities are indeed nonzero. The two events are also mutually exclusive, as only one Reaper can kill Fred; Fred can only die once. So the probability that Reaper 1 or Reaper 2 kills Fred is greater than the probability that Reaper 1 does. Ergo, the probability that Reaper 1 or Reaper 2 kills Fred is greater than But nothing can be over likely. Therefore, that Reaper 1 or Reaper 2 kills Fred is, yet isn’t, over likely. There’s our contradiction.

In fact, we don’t even need to assume there is a Reaper 1, though that simplifies the math. Suppose . Then as long as there’s a Reaper 2, we have that it’s over likely that Reaper 2, 3, or 4 kills Fred; to be exact, the probability is . And if there’s a Reaper 3, it’s over likely that Reaper 3, 4, 5, 6, or 7 kills Fred. And so on. Even changing does not necessarily rescue us from absurdity.

It’s problematic for Pruss if his scenario leads to contradiction in all these cases. His thesis is that the only available Inconsistent Pair response to entails, counterintuitively, that is impossible if but possible if . But if my previous argument goes through, there’s another response available to the UPD proponent: that is possible if and only if

, and
the Reapers are numbered , where .

I doubt if this proposal would strike Pruss as counterintuitive in the same way. It doesn’t have the prima facie odd consequence that the scenario is impossible whenever is 1 but possible whenever is 1.000001—or, more broadly, that a small numerical difference makes a big modal difference.

So on this reading of “[t]he probability that the Reaper’s swing would succeed in killing Fred is ,” fails to threaten the UPD. But I don’t think Pruss would have made such a glaring oversight in devising his scenario. In all likelihood, what Pruss means by “[t]he probability that the Reaper’s swing would succeed in killing Fred” is not the unconditional probability but rather the conditional probability . That is, he means the probability, conditional on the Reaper’s swinging at Fred, of the swing’s killing Fred. And if that equals , then the probability of the swing’s not killing Fred, given that the swing occurs, is .

Appendix B

If we’ve interpreted Pruss correctly, then, as noted at the end of the previous appendix, we have and, consequently, Pruss also tells us what the probability is, given an integer , that every Reaper beginning with Reaper fails to kill Fred, on the supposition that each Reaper in that subseries tries. He says it’s zero. Let’s see why that is.

We denote the event that none succeeds by , which is a more compact version of the infinite sequence of intersections Likewise, we write to denote the event that all Reapers beginning with Reaper swing, i.e., try to kill Fred. In probability/measure theory any event representable as a conjunction is the intersection of the events whose occurrence ’s conjuncts assert. With the information provided in we may deduce the conditional probability that Fred is not killed by the time Reaper would’ve swung—that all Reapers earlier than and including Reaper fail (that is, Reaper fails, Reaper fails, Reaper fails, and so on ad infinitum).

The probability

equals

on the assumption that, for any positive integer ,

(I’m indebted to ChatGPT for the insight that this assumption is necessary.) This last equation states that the probability that Reaper does not succeed in killing Fred, given that all Reapers earlier than and including Reaper try, equals the probability of the same given the same supposition plus the supposition that all Reapers following Reaper do not succeed. Does this equation hold? Honestly, I doubt it. Conditionalizing on the additional event that no Reaper succeeds in killing Fred after Reaper ’s attempt arguably makes a difference to the probability, in that it gives us reason to suspect no Reaper even tries to kill Fred after Reaper swings. For a Reaper likelier doesn’t succeed if it doesn’t try at all than if it tries. And if no later Reaper tried, that would entail that Reaper succeeds (on our assumption that Reaper tries, which means all earlier Reapers try and fail); otherwise, some later Reaper would try to make up for Reaper ’s failure. By this reasoning, it would appear the additional condition gives us some evidence against , lowering its probability.

The elephant in the room is that, by specifying that we have in mind conditional probabilities rather than unconditional ones, we have made all the more plausible the suggestion that these probabilities are subjective, or epistemic. Indeed, I’m not sure there is any precedent in the philosophical or mathematical literature for defining or interpreting conditional probabilities as objective, like the chance of a coin’s coming up heads supposedly is (as it’s not merely a matter of how confident one actually is or should be that the coin will come up heads, but of something independent of one’s mind and minds in general, like how frequently the coin would come up heads were it flipped infinitely many times). So, until someone goes to the trouble of elucidating what it might mean for a conditional probability to be objective, we had better stick with the conventional epistemic reading.

But suppose the foregoing equation is true, despite the worries I’ve raised. Then, to show , we need the further assumption that

equals

or, in more compact notation, . Essentially, we need it to be the case that, for any positive integer , once the occurrence of the Reaper’s attempt/swing is fixed, the occurrence of any other Reaper’s attempt makes no difference to the probability of the Reaper’s non-success. In other words, there must be no difference between and . But worries similar to the previous ones crop up here. Of course, something slightly different’s going on; we’re now comparing the probability that Reaper doesn’t succeed assuming it tries to the probability of the same assuming all Reapers earlier than and including Reaper (including Reaper ) try. The extra assumptions that appear in the latter probability’s condition have to do with attempts, whereas the extra assumptions we conditionalized on previously had to do with successes. Nonetheless, adding these assumptions seems to make a difference, supposing as we have been that these conditional probabilities are epistemic. In particular, we can be absolutely sure that Reaper fails to kill Fred if some later Reaper tries to kill him (and some later Reaper does given , provided that ). But assuming merely that Reaper tries to kill him, we can only have a credence of that Reaper fails. Admittedly, this doesn’t establish that the equation is false in cases where . But as long as it’s false in every other case, we have a problem.

Anyway, bracket all those concerns. Just take the equations for granted. We continue as follows:

For those who don’t know, I should mention that is like sigma, i.e., the summation notation , only it represents a product, not a sum. To calculate , we multiply all the values of resulting from assigning all values, one by one, in the interval

What is the value of this infinite product—this multiplication of infinitely many numbers? If we assume , the answer is easy:

In fact it’s trivial to calculate the product for any positive (or negative, for that matter) real value of , so long as In that case, for , we get , since one to any power is one. Thus:

We end up with zero once again. But what happens if our nonnegative integer is greater than zero? Then the smallest value of , in any multiplier of the form , is two or greater. Bearing this in mind, we can write a proof by cases that the infinite product is still zero provided that

Suppose In that case the result of is a positive fraction whose magnitude increases indefinitely as approaches infinity. But even though it increases indefinitely, it does not become arbitrarily large. It is always less than one. Now, if you take any positive number, and multiply it by a positive fraction less than one, you get a smaller number than you had initially. So with each new multiplier in the infinite product (starting from the multiplier , and proceeding to and so on), the product of all multipliers up to and including shrinks. Call any such product of all multipliers up to and including a given multiplier a “partial product,” as it is merely part of the infinite multiplication expression.

Not only does the partial product shrink indefinitely as multipliers are introduced, but its magnitude becomes arbitrarily small. (We’ll consider an argument for this momentarily, albeit a half-assed one.) That is, it gets arbitrarily close to zero. Thus, the infinite product is zero, as it is by definition equal to the limit of the partial product as goes to infinity.

How do we know the partial product gets arbitrarily close to zero as goes to infinity? This follows from the fact that, for any , you can get arbitrarily close to zero by multiplying by itself arbitrarily many times. For multiplying by itself arbitrarily many times is effectively what happens in the infinite product (and we’ve stipulated that , which makes ). We multiply by , and then multiply the result by , and so on. Put another way, we multiply by

Though , there can be no doubt that, if we multiply by (which is less than one), multiply their product by (again, less than one), and so on, then sooner or later we’ll get a number no greater than . And in multiplying by a bunch of numbers whose product is or less, we in effect multiply by itself or something smaller. Furthermore, given that this sequence of multipliers is infinite, we can be confident is effectively squared infinitely many times. It just takes more multipliers every time, since the farther along you get in the sequence, the closer the multipliers get to one, and the less the partial product shrinks with the introduction of each multiplier.

I’m aware this argument doesn’t really work, but it’s the best I feel I can do at the moment. (Of course, if there’s no legitimate proof to be given, that works in my favor, not Pruss’s.)

Previously we assumed for the sake of argument that We now imagine ourselves to have shown informally that, in that case, the infinite product is zero. Next, to complete our proof by cases, let’s assume . (That is less than one is the only possibility that remains, given our presupposition that ) Recall that Pruss stipulated So the exponent must be a positive proper fraction (In order for this fraction to be positive, it must be that and are both positive or both negative. But that’s not pertinent.) I’m no mathematician, so this is all I managed to come up with on my own. At least it’s semi-useful to the end of proving the desired conclusion. I had ChatGPT take care of the rest:

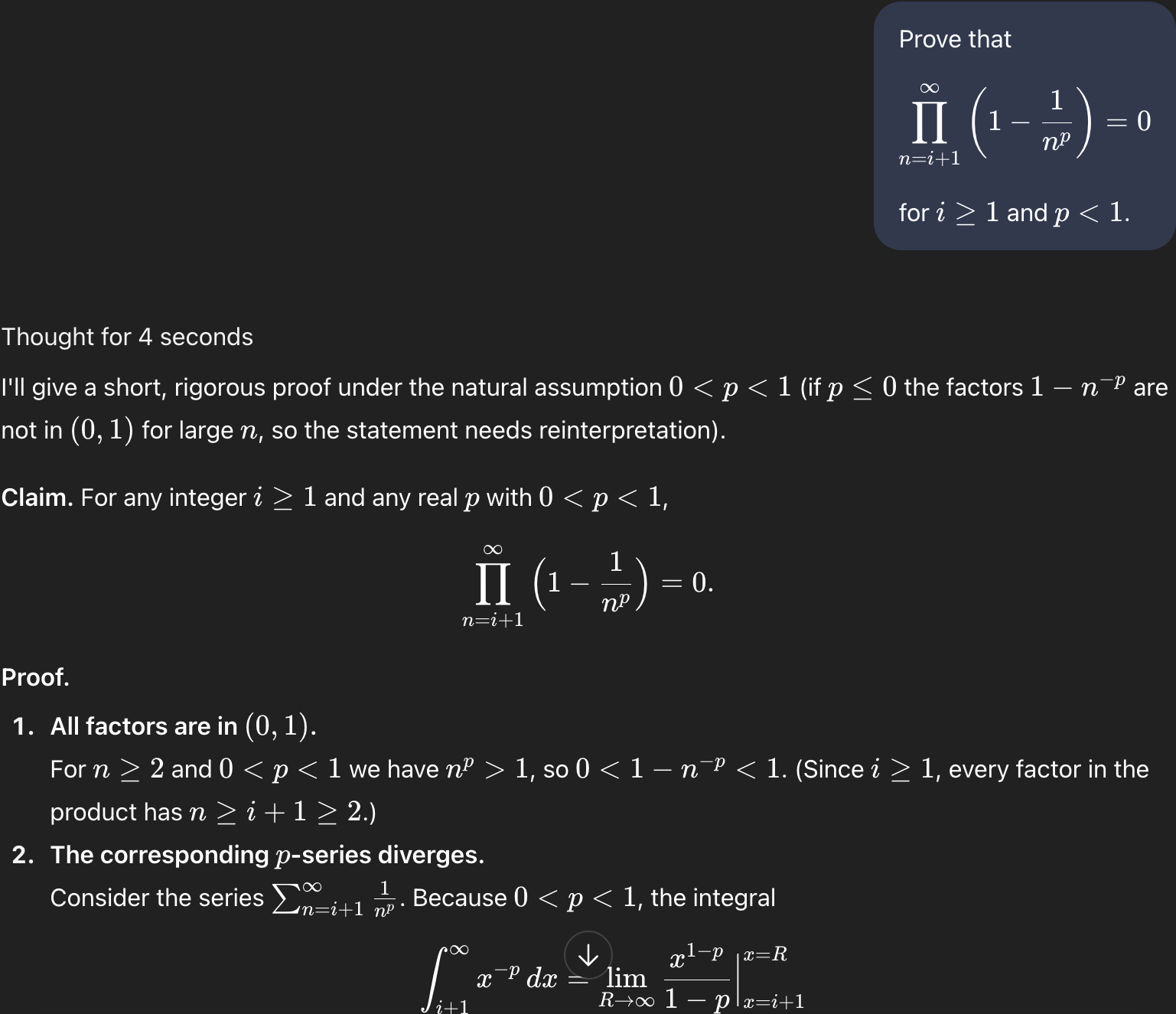
What’s neat is that, despite my forgetting to clarify my underlying assumption that , GPT picked up on the fact that such an assumption is appropriate in this context. This is perhaps a bit of evidence in favor of GPT’s possessing true intelligence and my lacking it.

If the above proof works, we have, for all ,

but what we want is

The way to reach this conclusion, presumably, is to establish that

and then appeal to the principle that a union of events, each of whose probabilities conditional on is zero, itself has probability zero given (assuming, as ChatGPT said we must, that no individual event in the union’s probability changes when we conditionalize on events with smaller indices in the union). I leave that proof as an exercise for the reader.