Computing the prime ideals in the ring of polynomials with integer coefficients

We’ll use ideas from an older post to compute all of the prime ideals in the ring . This is done in order to better understand the “arithmetic surface” .

Let’s get the easy stuff out of the way: since is an integral domain, the zero ideal is prime. Now suppose is a prime ideal which isn’t zero. Suppose is a principal ideal, with for some polynomial . Because is a unique factorization domain, this is equivalent to being -irreducible. By Gauss’ Lemma on polynomials, this is the same as being -irreducible and primitive in . Hence all principal prime ideals are exactly those that are principally generated by a -irreducible polynomial with coefficients in , written so that its coefficients are relatively prime.

Now suppose is a prime ideal which is not principal. We know from an older post that in this case there exists two relatively prime polynomials and that lie in . We know that these polynomials stay relatively prime when considered in the larger ring . This larger ring being an Euclidean domain, Bézout’s Identity is verified: there must exists a pair of polynomials such that We may put all coefficients that appear in and over the same denumerator , and write and for some . This gives the following equation in : Therefore is contained in the ideal generated by and , hence is contained in . Because is neither zero nor a unit in , it admits a decomposition into its prime factors, one of which must lie in because is a prime ideal. Thus contains at least one prime number .

Consider the map of rings which sends to . This is a surjective map, whose kernel is the prime ideal . Hence the map induces an isomorphism of rings Because is contained in , the prime ideal corresponds to a prime ideal in . Note that because is a principal ideal domain, we can write where is some polynomial in . In fact, as we’ve mentioned, the image of in the quotient is a prime ideal, so the element is an irreducible polynomial; without loss of generality we may suppose further that is monic, since the coefficient ring is a field. The polynomial in is its own representative when seen as an element of .

Let be the map used in the previous paragraphs. From the previous equation mod , we must have . In particular, this shows is a maximal ideal, since is a maximal ideal (every nonzero prime ideal in a PID is maximal). Also, it is not too hard to show by double inclusion that . Hence . We could also simply show that , and show that is a maximal ideal because the quotient is isomorphic to the field .

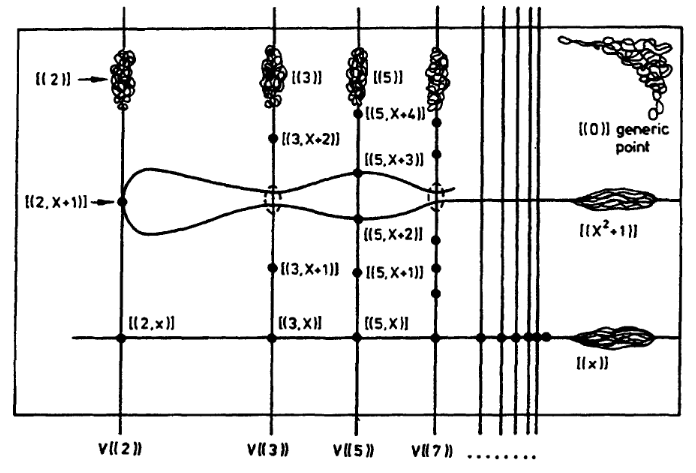
In conclusion, the prime ideals of are precisely:

1. the zero ideal ;
2. the ideals where is a prime number;
3. the ideals where is a -irreducible polynomial that is primitive, i.e. such that the greatest common divisor of its coefficients is 1; or
4. the ideals where is a prime number and is a monic polynomial which is irreducible modulo .

As in the case, the zero ideal is the two-dimensional generic point of the surface, the principal ideals are the one-dimensional points corresponding to curves, and the maximal ideals (those with two generators) are the “usual” zero-dimensional closed points.