My summary of the Min-Hu’s paper on Signatured Deep Fictitious Play. Signatures would be the key thing to speed up computations in a wide range of continuous time models in macro and finance.
Start with a bit of MFG background:
3 ways of formulating MFG with common noise:
inf-dim master equation, a type of 2nd order nonlinear HJB involving derivatives wrt probability measure. Direct simulation is infeasible due to the difficulty of discretizing probability space.
stochastic FP/HJB system, complicated form, forward-backward coupling, 2nd order differential operators involved
FBSDE of McKean-Vlasov type, generally requires convexity of the Hamiltonian
All 3 approraches require monotonicity to ensure uniqueness.
For numerical aspect, existing DL methods fix the sampling common noise paths, and solve corresponding MFG, leading to nested loop structure. Millions of simulations of common noise path needed to produce accurate predictions for unseen common shock realizations. Costly computation.
This paper: avoids solving any of the 3 approaches above, and no uniqueness issues. Single-loop DL algo.
Setup
fixed
: independent
-dim BM
: independent
-dim BM
Control problem:
Given initial , and a stochastic flow of prob measure , consider the problem:
s.t.
given
This is a control problem with random coefficient.
MFG definition a pair , s.t.
optimality: solves the control problem given
consistency:
is really a fixed point of
In extended MFGs, population effects also captured by , in addition to the marginal distribution of the states.
Signatures
path: , continuous mapping
signature of a path: a sequence of iterated integrals that encode the path’s behavior.
is an infinite series of tensors:
Here are generally tensors, with different dimensions, is a vector, is a matrix, is a tensor, etc
Denote as the truncated signature of of depth :
Traditional nested loop:
idiosyn BM paths common BM paths
For each of the common path , simulate paths of . Then, solve the problem associated to
This is my guess of the traditional approach:
Start with a guessed . Then fix a particular path. Solve for optimal control in along this path. In this step we need to simulate many idiosyn shock path.
Do this for many paths. Then, use the empirical flow of measures as the next guessed .
Sig-DFP Algorithm
Now:
where
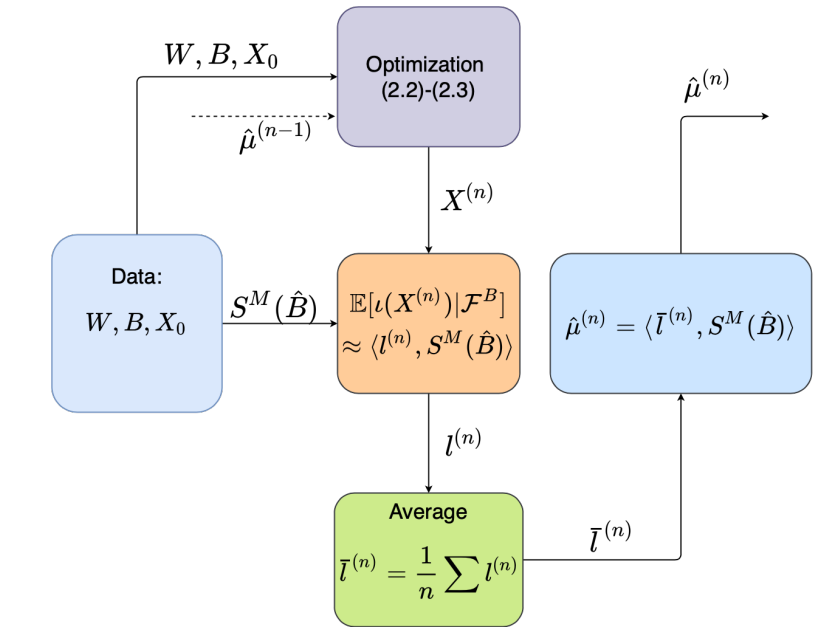
We specialize to the case where agents interact via some average: .
Given pairs of idiosyn and common BM paths
solve for by solving a discretized control problem, where the control , where denotes the NN map with parameters .
sample the optimized state processes , getting samples
obtain the linear functional above by implementing linear regressions. In particular, we pick 3 time indices, , and regress on
once is obtained, predicting for unseen common paths is simple: , .
after getting a new , we update our guess. Here, ficticious play uses a more modest updating, with old getting weight while new getting weight .
(But I find a more aggressive updating also works and is much faster)
Given the updated , we can compute the next iteration’s guessed flow of probability measure .
This is the basic idea. For extended MFGs, we’d need to propagate more than 1 conditional distribution flows within each iteration of fictitious play. For example, one used to forecast state the other used to forecast control, like consumption rate.
In the extended MFG of Cardaliaguet-Lehalle, there is yet another modification in that we need to forecast the LOM of , the aggregate trading rate, to forecast the stock price. But current stock price is based on the cumulative effect of past trading rates, not just the current trading rate.