Authorship claim
The text of this post, including the figures, is available openly
under the CC BY-NC-SA
4.0.
I claim, in good faith, that this post and the related
materials are a product of my own thought and work, that I did not omit
any references, that I am not aware of the existence of similar
publications and, that if similar publications exist, it is a
coincidence.
Intended audience
University students who have just started studying mathematical analysis.
Introduction
I was left with a feeling that I did not understand something about
derivative when I passed my last exam in mathematical analysis.
Eventually, I formulated what I did not understand and came up with
explanations on my own. This post is a result of my on and off thought
process over the course of about 4 years, between 2016 and 2020. It was
finalized in September 2020 and is published online for the first time
today the 27th of July 2024.
I do not have
explanations for some things still. If any edits are requested in the
comments, the commentators will be duly credited.
What is derivative?
Consider operation of division. How was it introduced in school? In school, we considered a cake which was divided on several pieces.
Let’s interpret the cake example differently. Assume, we have a shoelace instead of a cake. And assume we have a knife looking like an oyster fork (two-pronged fork) as in Fig.1.
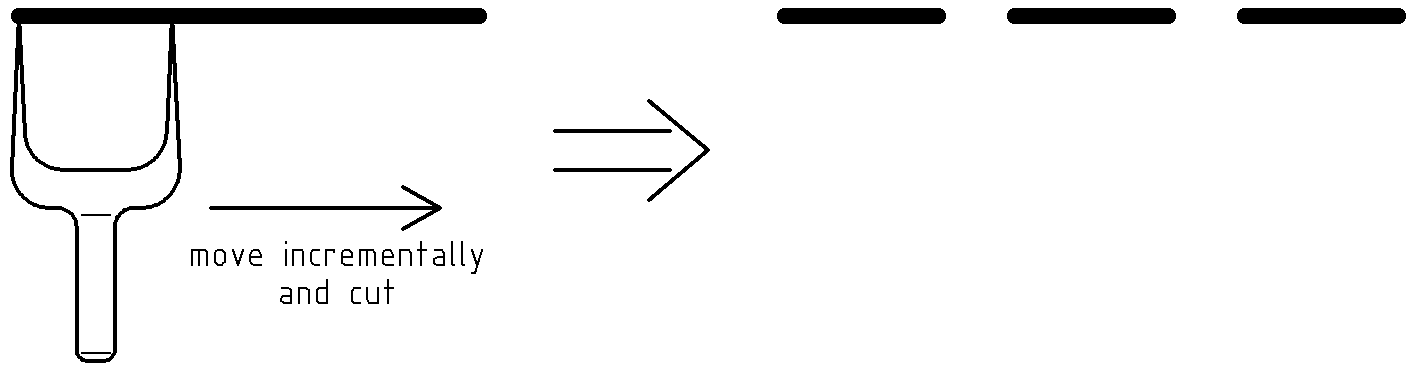
If the shoelace is straight and horizontal then we cut even pieces of it, provided that we move the fork-knife horizontally with equal increments after every cut.
Now let’s imagine the shoelace is not straight but curved instead as in Fig.2.
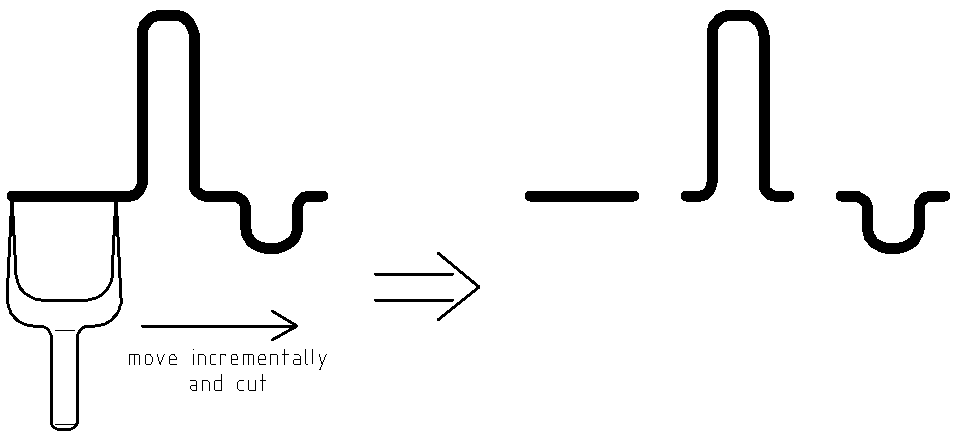
In this case, the knife-fork cuts out the pieces of different lengths.
Operation of division gives equal pieces as the result – this is the fundamental concept of division. This is the definition of division.
I can only divide the shoelace shown in Fig.1, I can’t divide the shoelace shown in Fig.2.
Let’s have a look at it from another perspective.
What does it mean to obtain equal pieces of the shoelace as the result of division?
Note that we divide the shoelace with fork-knife. In physics we always divide something with something.
I will not speak here about pure mathematical division like 10 / 2. because I do not know yet here how to explain it. We will be dealing with physical division when we know what physical parameters are involved in the division operation.
How do we divide the shoelace? We cut one piece, then we move the fork-knife to the right on a distance equal to its width and cut the second piece. And so on. If the shoelace is straight and horizontal like in Fig.1, we have got that the ratio of the shoelace’s piece to the width of the fork-knife is the same at each cut.
In turn, if we are dealing with shoelace shown in Fig.2 then we end up having that at each cut, the cut to the fork-knife width ratio is different.
This is what we really mean when talking about division.
Once again, it is important to emphasize that division, in fact, gives me the ratio between ONE SINGLE cut and the fork-knife width ASSUMING that all the other cuts will be equally proportional to the fork-knife width.
Pay attention that we are talking about ratio when dealing with division. The meaning of the word “ratio” will be clarified below in the paragraph about derivative.
The people who first came up with division started with simple things: straight horizontal shoelaces. But they realized then that there are shoelaces which are not straight and horizontal. And that they can no longer apply their rules of division to such shoelaces.
So what should we do if we want to divide the shoelace shown in Fig.2?
With the shoelaces it is not that obvious why would one want to think about it. But there are things in physics where we really want to know this.
For instance, I am making bigger and bigger distance every second when I am accelerating. Imagine now that my distance is a shoelace and my fork-knife has a width of second. So, I am taking second and begin cutting my distance with it. At each cut, the piece of the distance becomes bigger and bigger (but the width of my fork-knife – second – stays the same). Hence, the ratio of the piece to the fork-knife width is different at each cut. Therefore, I cannot use division to divide my distance by my time. But I want to do it in order to get velocity. And everyone who studies physics knows how important it is to be able to go between distance, velocity and acceleration.
Therefore, it is natural that it was Newton who first started thinking on how to divide the things that cannot be divided on equal pieces (there are doubts that it was Newton who came up with differential calculus, but until we know who it was let’s stick with Newton for simplicity).
So, what was Newton’s thinking process like?
We can imagine a shoelace and a fork-knife because these are physical objects. But what about distance and time?
It turns out that operation of division is only possible in a two dimensional space.
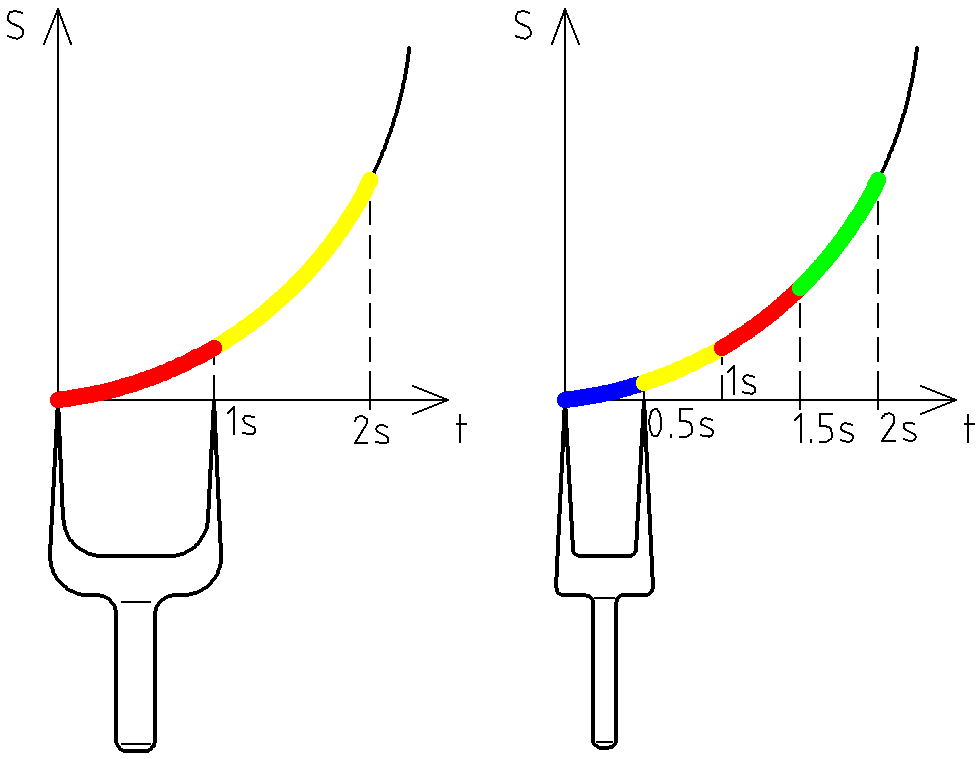
If I accelerate, I make bigger distance every moment – this ends up being a curve on an plane as shown in Fig.3.
As we discussed earlier, if I take a fork-knife of the width second (see the left half of Fig.3) and try to divide the curve with it, I will get pieces of different lengths.
Clearly, the yellow section is longer than the red one. Newton decided to try a fork-knife of a smaller width – may be the segments will be of more equal lengths.
On the right half of Fig.3, one may notice that if the width of the fork-knife is smaller, then the resulting sections are not that visibly unequal. It is not very clear that the blue and yellow sections are not equal.
The tendency is clear: the smaller the width of the fork-knife, the smaller the differences between the sections.
But the problem is that if we keep reducing the width of the fork-knife, all the sections will still be of different lengths even though the differences between their lengths will not be very big.
So, what can we do about it?
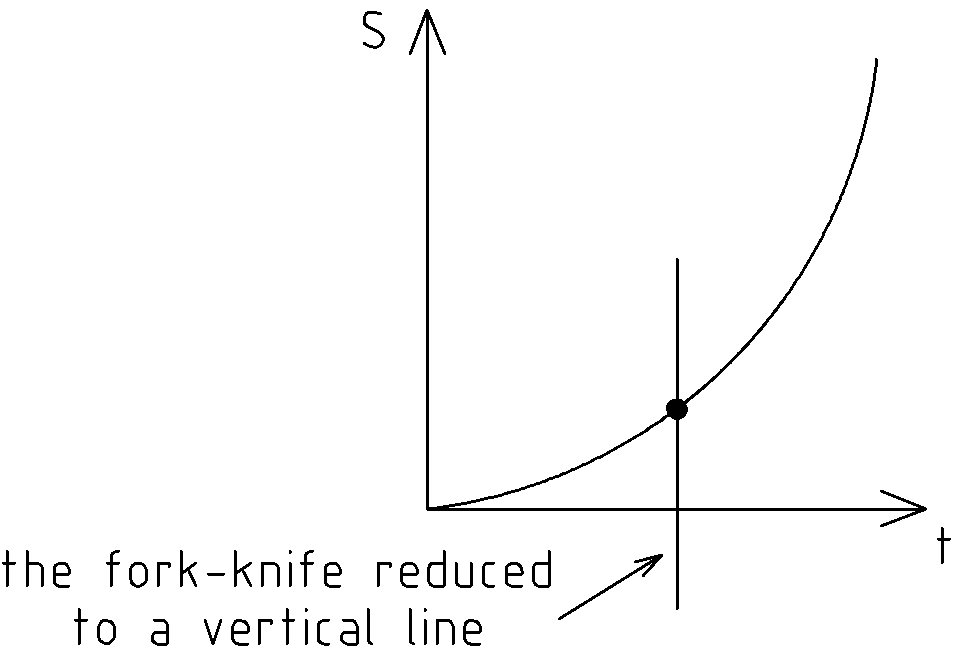
Let’s try reducing the fork-knife width to the minimum value possible – the width of a point.
Recollect how point was introduced in school. It was introduced as something infinitely small. What does it mean? It means that a point DOES have size but it is infinitely small. In other words, the size of a point is not zero, therefore we can reduce the width of the fork-knife to the size of a point.
If the width of the fork-knife is just a point, then cutting the curve (see Fig.3) with such a fork-knife will be the same as intersecting the curve with a vertical line (because the width of the vertical line is a point).
In this case we would say that the curve and the vertical line intersect at a point. But is it really true? Is the intersection really a point?
Let’s denote the size of the point as . We would usually say that the projections of the point on the and axes are also points. Let’s denote their sizes as and respectively. See Fig.5.
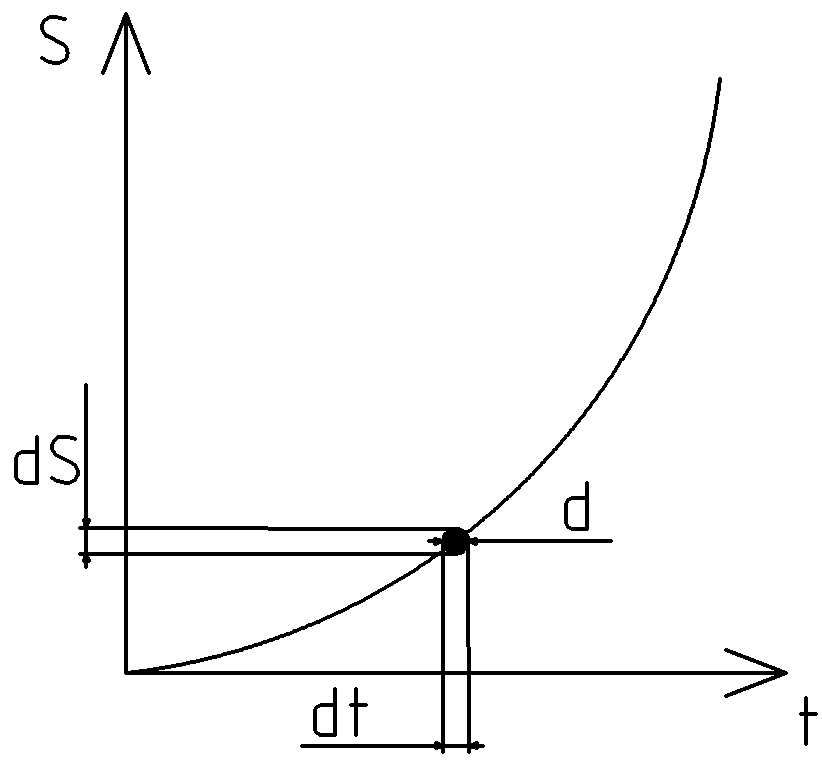
If both and are the points, then their sizes are equal. Therefore, their ratio must be : . But we know that is derivative and, obviously, the value of the derivative at the point shown in Fig.5 is not (i.e., the angle of inclination of the tangent at out point is not visually).
Hence, there is something wrong with it.
Maybe, the intersection of the vertical line and the curve is not a point? I know for sure that I have reduced the width of my fork-knife to a point. Therefore, is a point. I also know for sure that derivative at the point shown in Fig.5 is not (the angle of inclination of the tangent at out point is not visually).
Then must not be a point. This is the main concept of “derivative” – the curve and the vertical line do not intersect at a point.
How can it be?
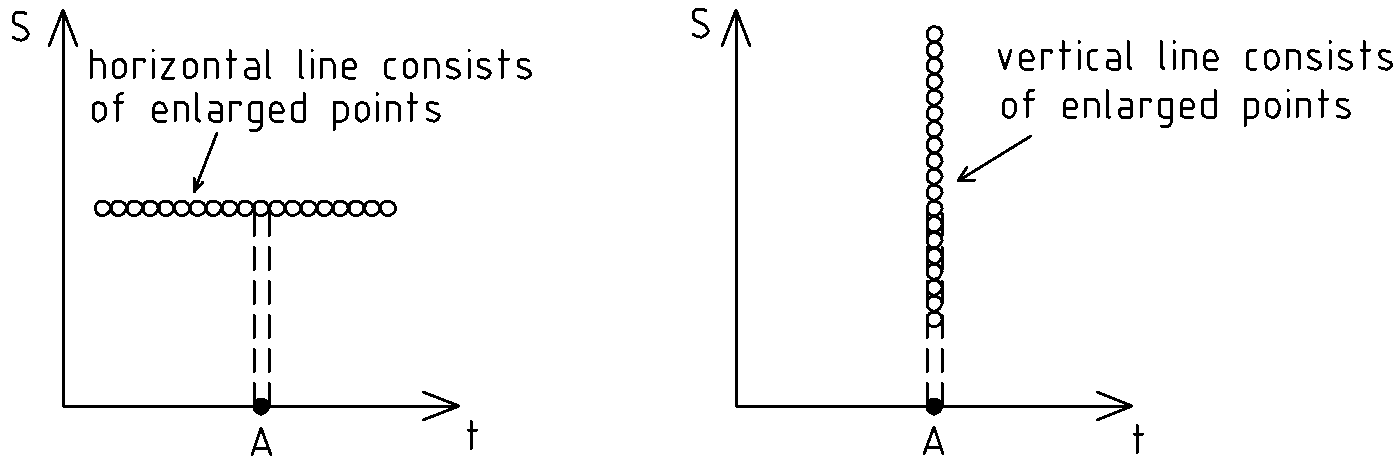
A point has a size. Let’s enlarge a point and consider two extreme cases: 1) a vertical line intersects with a horizontal line and 2) two vertical lines intersect.
See Fig.6. What we want here is to substitute the vertical line with its projection on the horizontal axis. This projection is obviously a point. Let’s call it point . Then we want to tell how many points of the other line (the horizontal one and another vertical line) falls on the point .
In case of the horizontal line, only one point of the horizontal line falls on the point . In case of the vertical line, all the points of the vertical line fall on the point (in other words, an infinite amount of points fall on the point ).
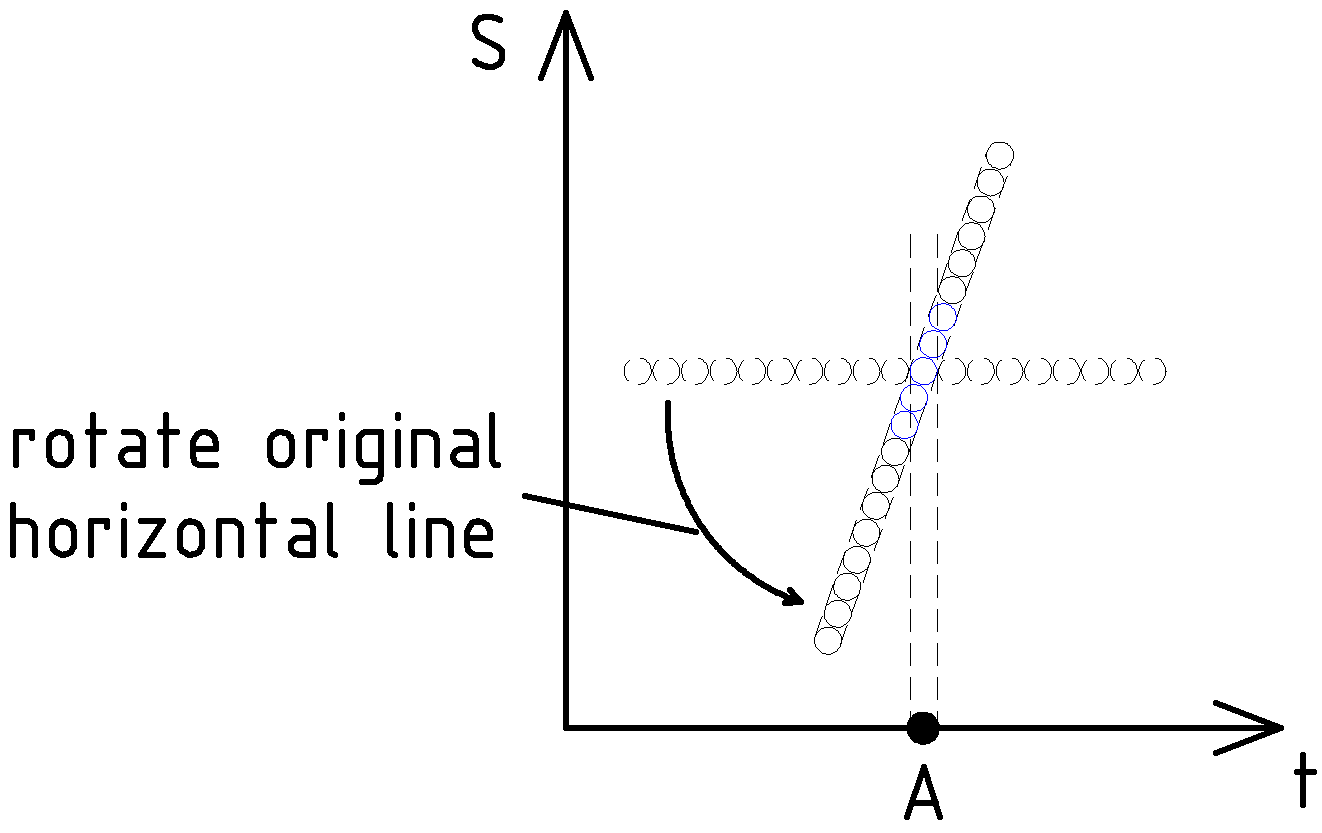
Now let’s intersect some straight inclined line with our main vertical line. In other words, we want to know how many of the inclined line’s points will fall on the point ?
The obvious deduction from the example with a horizontal and vertical line is that some finite amount – more than and less than infinity falls on the point A.
But how to explain this deduction? It is easy. The reason is that the points do in fact have some size. That means that we intersect not the lines that don’t have width, but rather strips of some width.
Now let’s draw again that vertical dashed corridor associated with the point – which, in fact, represents the boundaries of our main vertical line. Then let’s draw the dashed corridor representing the boundaries of the inclined line. Then let’s count how many points of the inclined line, in fact, fit into the intersection plane. See Fig.7.
In the Fig.7, we can see that five circles – highlighted in blue – fall into the dashed corridor above the point . It means that intersection of the vertical line and an inclined line – i.e. intersection of two straight lines at some angle between and happens along several points, not at one point.
The same holds true if we intersect a curve with the vertical line like in the Fig.5: is not a point there but, instead, several points. In Fig.5, several points of the curve correspond to a single point of the vertical line (i.e., to the projection of the vertical line on the axis ).
Therefore, when we say that a curve and a vertical line intersect at a point, we must add: “at a point on the horizontal axis”.
Now let’s recollect that we reduced the width of the fork-knife to a point. We still have the same problem: if I try to divide the curve from Fig.5 with such knife, I will end up having that at every cut the ratio of the points in the piece that is cut from the curve to the width of the fork-knife is different.
Therefore, Newton said that there is no way we can apply operation of division to curves.
Instead, let’s represent the curve from the Fig.5 as a set of pieces corresponding to every point on the axis . In other words, we take a point on the axis , we then draw a dashed corridor up to the curve, this dashed corridor cuts a piece from the curve. We do it for every point on the axis .
It is, actually, a common practice when dealing with discontinuous functions. For example, a discontinuous function is shown on Fig.8.
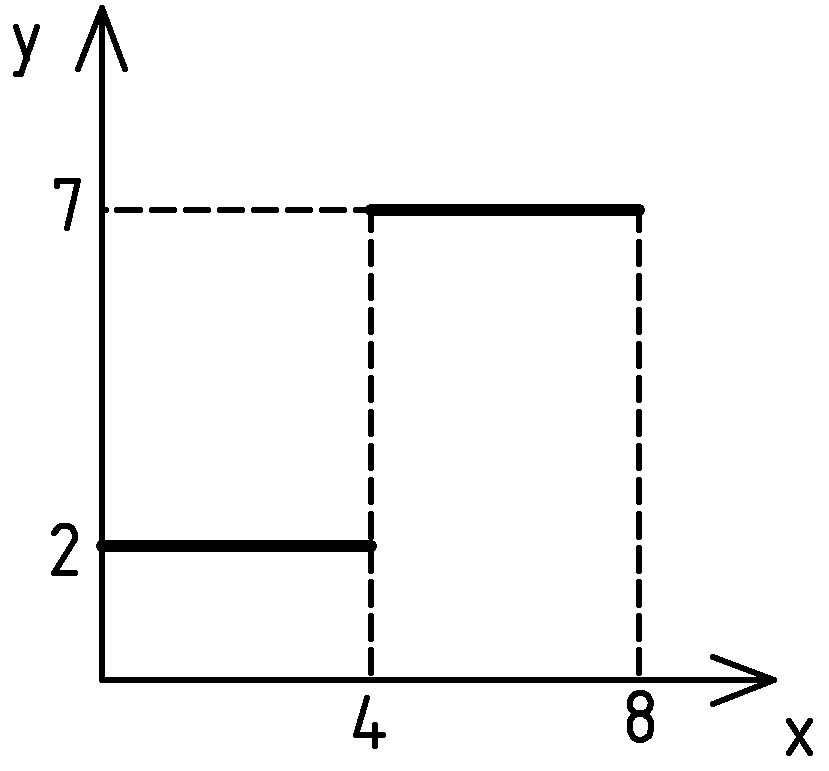
We formulate this function as:
We are following the same idea, but we define, for every point on the axis , how many points of the curve fall on the point on the axis .
Since we broke the curve on separate pieces, we can define division operation on each piece of the curve.
Now we have that for each piece of the curve, the fork-knife has the width of a point (fork-knife is represented by the point on the axis now). We stated that the fork-knife width cannot be less than a point. Therefore, if we use the point-width fork-knife to divide the corresponding piece of the curve, we will obtain only one piece equal to the length of the piece of the curve for which we are conducting the division operation. In other words, the result of division in this case is the ratio of the points in the curve that fall on the corresponding point on the axis to the one point on the axis.
For example, in Fig.7 we have point . The piece of the inclined line corresponding to point is shown in blue. We conduct the division operation on this piece. We take the fork-knife represented by the vertical dashed corridor associated with point . We cut our blue piece of the line with this fork-knife and we get the blue piece of the curve. We have not gotten several pieces after the division but, instead, we just got one piece – the same piece which we tried to divide. It is similar to division by – you always get the same number as the one you have tried to divide.
This is what derivative is. It is a real division operation specified on a piece of curve, which gives the ratio of the points in the piece to one point on the horizontal axis as the result.
We write derivative as .
Here is the point on the axis.
– attention – is the projection of the blue points (see Fig.7) on the vertical axis, i.e. how many points along the vertical axis our piece of the curve occupies.
Now notice, how we defined the function from Fig.8. We defined it as a table: for each section of the axis we know the value of .
But if each of the sections on the axis is shrunk to a point, then we will have an infinite number of entries in our table.
We need such a table when we define operation of division for a curve as was described above:
But in this case, I can construct a function because I know the values of at each point on the axis. For example, .
In other words, if the curve is continuous as in Fig.5 – as opposed to a discontinuous line as in Fig.8 – the table with which we define the curve gets converted into a function.
Yet in other words, continuous function is just a table in which the width of the section on the horizontal axis equals to a point for each entry in the table.
Now, I shall, briefly, touch on the topic of the size of a point. Here confusion can arise from the fact that everybody says that a point does not have a size and that it is infinitely small. However, I showed above that a point must have a size.
I think that the idea that a point does not have a size is erroneous. My question is how we pick the size of a point and what infinitely small means.
To answer this question we need to refer to the definition of the limit also bearing in mind how it kicks into the definition of derivative of a function. I am not going to cite it here, I presume the reader knows it exceptionally well.
We say that there exists some numerical value such that when the change in the coordinate becomes less than this numerical value , the corresponding change in the function divided by achieves some constant value.
Let’s write it mathematically for better clarity. Let’s say we have a function and want to take its derivative which, in turn, is given by:
Let’s say now, that at every point , we have a function
I.e., is a parameter (a constant) in , and is the variable. And as I have reduced below some numerical value , does not change with any more (at least visually) by the definition of limit. We say then that is just a point now. This can be point in figures 6 and 7.
In other words, this parameter determines when the line segment of finite size becomes a point. That is why any point has a size, I think.
But we picked the value of based on subjective visual observation of when the curve stops changing much with . Well, another chap with a different perspective could pick a smaller or bigger value for and the size of the point would be different then.
So that everyone could agree on the size of , we want to make as small as possible (so that it would be obvious to more and more people that the function does not change much visually). But we cannot make so small such that because we cannot perform division then: there will be nothing to divide the change of by as well as there will not be a change of :
This is what infinitely small means: a point must have a size as small as possible, but never zero. Zero is not a size - it is nothing. That is why a point cannot have zero size, but it can be close to it. How close?
I think it depends on the application. We choose the value of based on our application. If in our application is almost horizontal, can be huge. If in our application is very steep, must be tiny.
One might ask then: what about the space. The space is an infinity of adjacent planes, every plane is an infinity of adjacent lines, every line is an infinity of adjacent points. That is what we learn in the first lesson of geometry in school.
First, it is obvious now that a point must have a size, because if it is zero, one will not be able to stack points in lines, lines in planes and planes in the space. Second, but if the size of a point is different and depends on the application, then the size of the space will be different.
I would argue that we are never interested in space itself. We always consider some functions in space. And that is where the dependence of on the application kicks in.
And the cherry on the top is that we, actually, never worry about the value of . The mechanism of limit takes care of it and, simply, gives us some value for the limit we are calculating. I cannot understand how this happens. This looks like magic to me. I am still thinking about it.
Data availability
The figures are accessible at the following links: figure 1, figure 2, figure 3, figure 4, figure 5, figure 6, figure 7, figure 8. All figures were drawn in LiberCAD.