How to Decentralize L2s on Kaspa in the Post-Crescendo Pre-ZK Era (KIP-15 for dummies)

The post-Crescendo pre-ZK era will start as soon as the Crescendo update goes online and, as indicated by the name, will end sometime in the future with the activation of a (yet to be planned or named) hard-fork that will implement opcodes for validating ZK proofs.

However, Kaspa’s pruning means that L2s have to deal with data retention. ZK proofs provide terrific solutions (in fact, that was one of the main motivations to develop them), but we do not want to rely on their development for deploying smart-contracts. Hence, an interim solution is required. A solution that might have some drawbacks, but could provide scalability and decentralization for at least a few years, allowing to design and develop ZK opcodes carefully, rather than rushing them.

This is the purpose of KIP-15: to use the facilities already available in Kaspa to roll out L2s over Kaspa. In this post, we explain the problem in some more detail and describe how KIP-15 solves it.

Background

As most of you probably know, the Crescendo hard-fork will be activated soon. Crescendo introduces many interesting updates, but ZK opcodes are not one of them. ZK opcodes are extremely useful for facilitating smart contracts, but not strictly necessary. KIP-15 provides a neat interim solution for implementing L2 rollups over Kaspa without before ZK. To understand KIP-15 properly, we first need to understand the problem it solves: that L2s have to somehow deal with Kaspa’s pruning.

Pruning means that sufficiently old transactions (currently 52 hours old, but Crescendo reduces it to 30) and most sufficiently old block headers are removed from storage. Pruning is an absolute necessity, and it is the reason Kaspa nodes maintain low storage requirements despite the network running on high throughputs for years.

Data Availability

The data availability problems that arise from pruning are relevant to all forms of smart contracts, including on-chain execution. However, this post focuses on rollup-based architectures, as this is the direction Kaspa is heading.

Pruning makes sense for transactional layers: once all transactions are processed, the UTXO set contains all required information for validating transactions. The purpose of keeping transactions at all is to recover from reorgs, and make recent activity auditable for any full node (rendering attempts at passing invalid transactions detectable by the entire network, and retroactively provable). However, once processed, the transaction data is not needed to process new transactions.

This is no longer the case for smart contracts.

Rollup layers typically communicate with the network in two ways:

Payloads: arbitrary pieces of data attached to transactions. Payloads are opaque to the base layer, and it is the higher layer’s responsibility to parse them. The base layer sequences these payloads in the sense that it provides guarantees about the order in which these payloads were posted.
ZK-proofs: black magic that allows network nodes to easily verify arbitrarily complex computations.

Remark: This description is not very accurate. There are designs such as enshrined rollups that allow (but do not require) base layer nodes to audit the L2 execution, and to me, it seems that Kaspa is going in these directions. However, since this post is concerned with data availability, it does not really matter how the payloads are used, just that they are needed. Rollups that use ZK for settlement are usually called ZK rollups, whereas rollups that rely on the network for consistency and provide a protocol to resolve disputes on-chain are usually called optimistic rollups.

Unlike the case for UTXOs, when higher layers are in play, we cannot make any assumptions about the need for old data. There are many cases where to compute the next stage of the computation, we will have to refer to arbitrarily old payloads. Today’s transaction might rely on a piece of information that was posted to the network two years ago. So our task is to resolve the tension between pruning data for the sake storage requirements, and retaining data for the sake of arbitrarily complex dependncies between transactions.

So that’s the million-dollar question: how do we refer to data that has already been pruned? ZK opcodes provide elegant solutions to this problem. They allow creating a short efficiently verifiable (though heavy to compute) proof of arbitrary statements such as “the transaction in block X had payload Y”, and recursively compose them to a single proof of the entire state of the network (there are obviously a lot more details to this than I am letting on, but that’s for another post).

But we don’t want to wait for ZK opcodes to be available before rolling out smart contracts. This is the motivation for KIP-15: coming up with an interim solution that can remain scalable for a few years, allowing the community to concurrently develop ZK opcodes and deploy smart contracts.

Archival Nodes and ATANs

The most straightforward solution is to have all L2 nodes maintain an archival node that stores the entire transaction ledger since the L2 was launched.

This is unreasonable. At full capacity, the Kaspa ledger grows by more than 100 gigabytes per day. Running an archival node is highly expensive, and, since archival data is required to validate the L2 state, using archival nodes will make syncing new nodes increasingly slow and computationally heavy. A new L2 node would have to download the entire ledger since the L2 launched, and process the entire history of the L2, just to validate the current state of the network.

KIP-15 – written by Roman Melnikov and Mike Zak of Igra Labs – proposes a middle ground: accepted transaction archival nodes, or ATANs for short. An ATAN stands between a (pruned) full node and an archival node. It does not store transaction data, but it does store enough data to validate the publication of any transaction. Moreover, given two transactions, one can also validate the order in which they were processed.

The key observation is that to do this, we do not need to store the transaction data, only the hashes of transactions. Smart contract transactions can be quite bloated: DeFi transactions over ERC-20 tokens can often weigh two kilobytes and beyond. A transaction hash, on the other hand, is always 32 bytes long (for most hashes, and in particular the blake2b hash used by Kaspa for computing transaction IDs), making the compression quite effective.

How effective? According to estimates by Igra labs, the storage of an ATAN is expected to grow by at most 5 terabytes per year. That is, even if it takes ten years to implement ZK opcodes (and it won’t, it will happen much faster), storage requirements for ATANs remain within reason.

This design becomes more compelling if we remember that for an ATAN to index an L2, it only needs to run since the L2 was launched, and can prune all previous data. Moreover, it is likely possible to modify an ATAN to only keep track of data relevant to a particular L2 and discard the rest (though this is trickier than it sounds, e.g. how can you verify that such a partial ATAN did not censor transactions?).

The Nitty-Gritty

In the second part of the post, we dive a bit into the Kaspa components relevant to KIP-15, and then explain what ATANs do differently.

Merkle Trees

As you might know, Bitcoin and many other chains store something called a transaction Merkle root in each block header. If you don’t know what Merkle trees are or how they are used in cryptocurrencies, then I highly recommend that you fill that gap (e.g. by reading the relevant appendix in my book). But here are the key facts you need to know for now:

A Merkle tree encodes an arbitrarily long list of items into a single 32-byte hash called the Merkle root.
When computing the Merkle tree, we also compute for each list item a Merkle proof. The Merkle proof and Merkle root together can be used to prove that the item was in the original list.
Moreover, given two Merkle proofs, we can tell which item was added first to the Merkle tree (assuming we agree on the order the Merkle leaves are populated, e.g. from left to right), giving us ordering guarantees.

Remark: the size of the Merkle proof is logarithmic in the number of items, which means that it increases by a single hash every time the list is doubled. You need zero hashes for one item, one hash for two items, two hashes for four items, three hashes for eight items, and more generally hashes for items, or equivalently, hashes for items.

AcceptedIDMerkleRoot

Merkle trees have been used in Bitcoin since before it was launched, they are used to tie the block data to the block header. On the one hand, we want the header to be small, but on the other, given the data of the corresponding block, we want to make sure that it was not modified or tampered with. We can do this by computing the Merkle tree of all transactions, and verifying that its root matches the Merkle root stored in the header.

Another use for the Merkle root is to easily prove that a transaction is in a block. If I only have the block header, and you want to prove that some transaction was included in a block, all you have to do is send me the Merkle proof for that particular transaction.

In Kaspa things are a bit different. We use Merkle trees for block validation exactly like in Bitcoin. However, when it comes to proving the existence of a transaction, we actually want the block to contain other data: the confirmed transactions in the so-called “merge set” of the block.

Recall that in Kaspa each block has a selected פarent: the parent with most work behind it. Similarly, the heaviest tip is called the selected tip, and the chain obtained by starting from the selected tip and traversing to the selected child all the way to genesis is called the selected chain. The blocks “between” a block and its selected parent are called the merge set of .

All of the above is summarized in this diagram: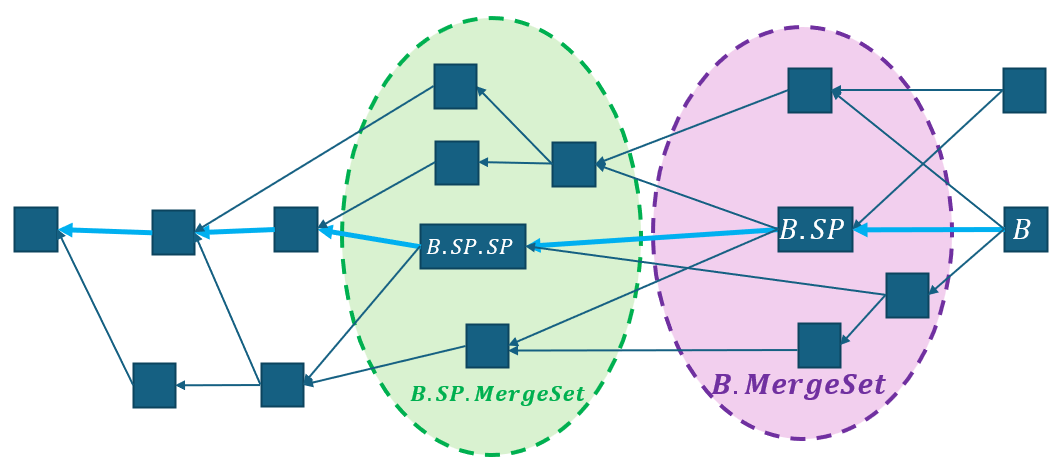

In Kaspa, the header of the block contains two Merkle roots. One is exactly like in Bitcoin, and is only used to force the header to commit to a particular set of transactions. However, unlike Bitcoin, from the point of view of these transactions have not been processed yet. Instead, when the block is processed, only the transactions in are processed. The GHOSTDAG protocol is used to order , extract the transactions therein, and resolve all conflicts. The transactions that survive the conflict resolution are then placed into a Merkle tree whose root is stored in a field called .

Note that delaying block processing is a necessity. Imagine there is a block that contains a transaction , and a parallel block that contains a conflicting transaction . The GHOSTDAG ordering will eventually determine whether or (or some other transaction conflicting both) will be accepted, and that ordering is yet to be determined at the time was created. More plainly speaking: when a miner creates a block, they can not know which of the transactions therein will be included. Determining this is delegated to a future block.

Using a Merkle root of the entire merge set for each block naturally complements the way the GHOSTDAG ordering converges, and has other useful properties:

It makes it so that to compute the state of the network, we only need to traverse the selected chain (and not the entire DAG.
It allows us to avoid many heavy computations, and only perform them for blocks on the selected chain

Pruning and Posterity blocks

Pruning in Kaspa is complicated, and is well beyond the intentions of this post (there aren’t good accessible sources on that yet, though it is definitely on my list. For now, the second half of the GHOSTDAG 101 workshop I gave ages ago somewhat fits the bill, though I would explain a lot of the content differently nowadays.) We list a few facts key to the discussion.

Kaspa erases all block data below a certain point called the pruning point. The pruning point is a block on the selected chain that is chosen uniformly for the entire network. To verify the weight of the chain, kaspa nodes maintain something called a NiPoPoW, which is a DAG adaptation of the MLS protocol.

Additionally, Kaspa nodes store so-called posterity headers: a sparse chain of headers (currently spaced 24 hours apart), identically chosen for all network nodes, from the pruning point to genesis.

Currently, pruning blocks act as posterity blocks, as they suit all the required properties.

Remark: Accordingly, most texts (including KIP-15) refer to them plainly as pruning headers. However, since these are two different roles that could be decoupled, and the posterity headers and their frequency could be chosen completely arbitrarily, I prefer to make the distinction.

The key facts about posterity blocks are:

Each block points to the previous posterity block (kind of, in practice it points to the previous previous previous posterity header, because reasons. But we will ignore that).
The previous posterity block of each block is on its selected chain.
The posterity chain is the one obtained by starting from the current pruning block and traversing to previous posterity blocks, all the way down to genesis.
The pruning block is always on the selected chain of the selected tip, and for each block, the previous posterity block is on its selected chain
All nodes have the same posterity blocks.

This is summarized in the following diagram: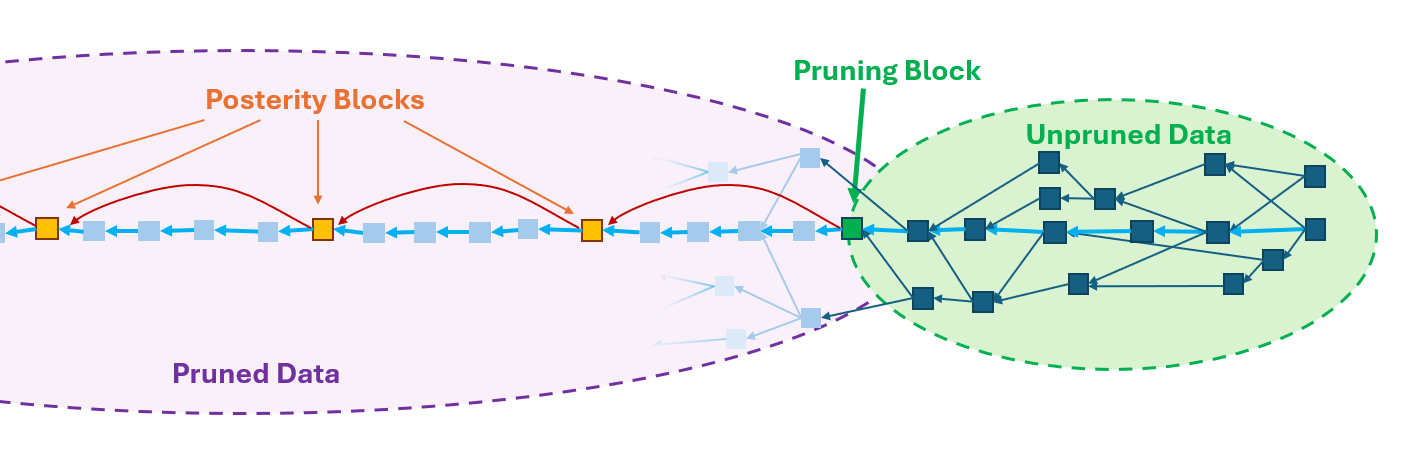

Posterity blocks are the key to syncing ATANs efficiently and trustlessly.

Merkle tree Sorting

As briefly mentioned before, Merkle trees carry a bit more information than just what elements they encode: an ordering. Given two Merkle proofs for two transactions, we can tell which transaction was entered into the Merkle tree first.

Unfortunately, transactions are not entered into the Merkle tree in the order they were processed. In fact, there is no relation between the arrangement of transactions in the Merkle tree and the order in which they were processed. The reason for that is a great example that sometimes too much foresight can be a bad thing.

When designing this part of the consensus, someone had a clever idea: instead of using the processing ordering, let’s order the transactions by their hash, from lowest to highest, and add them to the Merkle root in this order.

Why? The idea was that this would allow a simple proof of non-inclusion. If you want to show that a transaction with hash was not in a block, it suffices to show Merkle proofs of two adjacent elements with hashess and such that . That way, we know that there is no room for . (If we have a sorted list of numbers, and we know the numbers and are adjacent to each other on this list, we can conclude that is not on the list without checking the rest of the numbers).

This feature of Kaspa was never actually used, but implementing it had the consequence that, from the point of view of a pruned full node, the exact order in which transactions were processed is lost to time.

As we explained before, when in a UTXO mindset, this is hardly a loss at all. Two parallel transactions are either conflicting or independent. In the former case, we only care which transaction survived the conflict resolution, and in the latter, we don’t care at all. As long as all conflicts are resolved the same, the final state will turn out the same, regardless of the processing order.

This no longer holds for smart contracts. The result of processing a smart contract transaction can, and often does, depend on the processing order of two or more old transactions.

The ATAN approach is to do away with this by-hash ordering, and instead use the Merkle tree to commit not only to the transactions, but also to the order they were processed.

Note, however, that a part of validating a block is to verify that the AcceptedIDMerkleRoot is computed correctly. Changing the rules for computing AcceptedIDMerkleRoot means changing the definition of a valid block, making this change a hard-fork.

Remark: I was asked several times about this post that criticizes using sorting Merkle trees. This is an interesting piece, but it is irrelevant. First, note that this post talks about proof of non-membership, while ATANs do not prove non-membership. But even if we do want non-membership, the security concerns in the post are relevant when the Merkle tree is created by a non-trusted entity. Since in our setting, the entire network validates that the Merkle tree was computed correctly, we can trust that it is accurate, alleviating the concerns in the post.

KIP-15

With all this groundwork, we can finally specify KIP-15.

Consensus hard-fork

KIP-15 suggests removing the AcceptedIDMerkleRoot field, and replacing it with a new field called SequencingCommitment which is defined as follows:

Let AcceptedIDMerkleRoot contain the same transactions as before the hard-fork, but in execution order
For a block , define as where is the same hash used throughout Kaspa for Merkle trees (currently blake2b).

ATAN storage

An ATAN stores:

The headers of the entire selected chain
The hashes of all transactions

Say that each block contains about 200 transactions (reduced from the current 300 txn/block estimation to account for the fact that SC transactions are typically bigger), since we only store hashes, this comes up to about 64 kilobytes per second. The selected chain headers increase this by a little bit, and there is some more overhead, so let us say the storage increases by 100 kilobytes per second. This is equivalent to about 3.2 TB per year. The Igra labs estimates, which are probably more accurate, are three times higher than that.

Transactions vs. Transaction Hashes

Sharp readers might notice a discrepancy between how I described an ATAN and how it is described in the KIP. In the latter, the transactions themselves are stored rather than their hashes.

We initially set two goals for an ATAN: that it allows proving transaction processing and ordering indefinitely, and that it can be efficiently and trustlessly sync from a synced ATAN (with the help of a (pruned) full node). For the first goal, we do not even need the transaction hashes: selected chain headers are enough.

We will soon see that for syncing nodes, it suffices to store the transaction hashes, and not the transactions themselves.

So why do we consider storing transactions at all?

Well, remember our original motivation: we want to validate L2 transactions, and for that we need the history. We can now debate on whose responsibility it is to keep the history. But the key point is that ATANs can operate without them, leaving the choice to the network. In other words, it decouples maintaining the data from maintaining the ability to verify its authenticity.

Consider, for example, an archival node operator. Currently, in order to be able to keep arbitrarily old data verifiable, the archival node must archive the entire ledger history. After KIP-15 is implemented, they could use the ATAN to maintain the ability to verify, but use much cheaper storage solutions, such as backup tapes, to store the transaction data itself. The ATAN will maintain all transactions forever verifiable, and should the need arrive to recover a transaction, it could be pulled from deep storage and validated against the ATAN.

Similar ideas can be used to optimize ATANs used as nodes for one particular L2. They could only store transactions that are relevant to their network. This is tricky, as the L2 would have to provide some way to deal with attempts to censor transactions (how can you be sure that the node maintained all relevant transactions?), but before KIP-15 it would not have been possible.

Syncing an ATAN

Finally, we describe the process of syncing a new ATAN. For a decentralized trust model, we must require that a new ATAN could sync from an existing ATAN and a (pruned) full node. Alice need not trust Bob’s ATAN and, if she doesn’t trust the full node, she could sync one herself.

Say that a newly created ATAN Alice is syncing from an already existing ATAN Bob. They proceed as follows:

Bob sends Alice , where is a sufficiently old posterity header
Alice verifies that the Kaspa node knows of a posterity block whose has is (she can also verify that this block is older than the launch of the L2 she is synchronizing)
Let be the pruning block of the Kaspa node, and , let satisfy that . For going from down to do:
1. Bob sends Alice:
  1. the hashes of the transactions in in the order they were processed
2. Alice uses the transaction hashes to compute . If Bob is truthful, then it should be identical to .
3. Alice computes as .
4. If then Alice aborts, otherwise the protocol continues
Alice accepts

Note that Alice did not have to trust Bob in any step of the way, which means that the trust model of ATANs is similar to that of the underlying network.

In the KIP, the synchronization protocol is slightly different: Bob sends Alice the transactions themselves and not their hashes. This relates to the discussion we had above. In the KIP variant, Alice would first hash all transactions, and then use these hashes to compute the Merkle root. In particular, knowing the transactions and not just their hashes does not provide any added security, while it does force Bob to store all transaction data.

Conclusion

There is a small caveat to that. An ordinary user who does not want to sync an ATAN will have to trust that they have access to properly synced ATANs. This is not too different than a Kaspa/Bitcoin user who trusts public nodes for ledger data. What makes or breaks this trust model is the intensity of running a node. If nodes are sufficiently light to provide ample sources of truth, then we can consider the trust model sound.

ATANs are noticeably heavier to sync and operate than full nodes, but are magnitudes more efficient than archival nodes, providing the L2s with the same amount of decentralization you would see on networks with moderately heavy nodes. I would argue that an ATAN based L2 could easily become more decentralized than Solana, or Ethereum L2s.

Existing networks such as KRC-20 (which, last time I checked, uses archival indexers of which there are very few) can (and, I think some plan to) adopt ATANs as well to improve the trust model and decentralization.

In general, ATANs allow maximizing L2 decentralization and trustlessness as much as possible without using ZK, while keeping storage and computational requirements somewhat above the base layer, but still very much within reason.

Composing this post required three workdays worth of research, writing, and editing. If you want to help me consistently create quality content, please consider supporting my work.