Tiny Time

Tiny time on my mind..

Let’s start with the basics:

The thing that really got my attention initially was the fact that:

I do not understand how the tiny formula works or how it was derived..

Why not ? Or ? (Do these other formulas give us anything interesting? 🤷‍♀️)

Regardless..

The 1d up/down-ness inside the black hole really got me thinking.

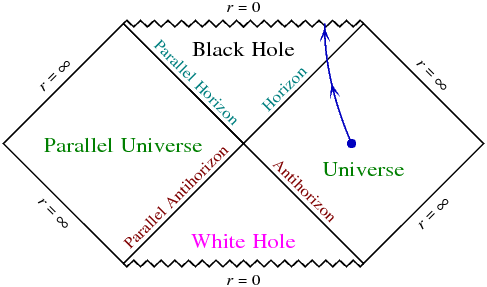
At first I had the idea that if we took that parallel universe out of there & wrapped our universe around to the otherside, we’d have a nice cylinder (& some nice possible photon interaction from the photons coming from the “parallel antihorizon” & “antihorizon” lines). Maybe connect the white & black hole so we have a nice torus. 🤷‍♀️

After thinking about it for a bit, I thought of a slightly different model.

What if the point at the bottom is the white hole, the point at the top is the black hole & the rest is our universe? In the diagram, the white hole big bang is a singular point (0d), as is the black hole. All light emitted from the white hole would eventually reach the black hole (& in an instant according to the photons that make the full trip).

Based on my primitive understanding, I think if viewed from a time reversed frame of reference, the black hole would become the white hole & vice versa.

Yet I digress..

In the video, he mentions that there is acceleration (of time!) with movement. The tiny function doesn’t produce linear growth. Interesting.

Also, because wordplay is amazing, I find it very interesting that we could view as the event horizon (of numbers). As in once u pass the event horizon.. it’s over.

There is also the inner event horizon (of games?) & on the opposite end of the tiny spectrum we have .

What is beyond the inner event horizon? Pure speculation: a simple point. That is to say, a 0 dimensional object. In 0d, there is no time or space (at least in the classical sense). It gets even weirder in d. Perhaps a rather pointless (& seemingly paradoxical) dimension..