I’m looking at Theorem 13.26 of (Muscat 2024), Taylor Series. We are given a function which is analytic on some open subset of the complex plane, which I’ll call U. We also have a bounded, linear operator , assumed to be a member of the Banach Algebra for some space .
Then we are shown:
What’s going on here? There’s the inverse of an operator embedded in the integral, and somehow we are integrating over values of along a circular path: this circular path is a subset of the complex plane.
The integral is known as the Dunford Integral and forms part of the functional calculus (dealt with in Chapter 14 of the book).
The idea is to take the function and the operator and combine them into a new operator, . This new operator is, like , a member of and so . The combination means the existing function , which works on scalars, is adapted to an operator which works on the space ; the close link is why the same letter is used for both.
The combination is made through multiplying the function by the term . This latter term is the inverse of an operator, an operator determined by the given value of . The interesting point, not covered yet in the book, is that the inverse of may not exist for certain values of : these values form a subset of the complex plane known as the spectrum of T, denoted .
The above has highlighted three subsets of the complex plane which are relevant to understanding the definition of . It’s worth sketching out their geometry:
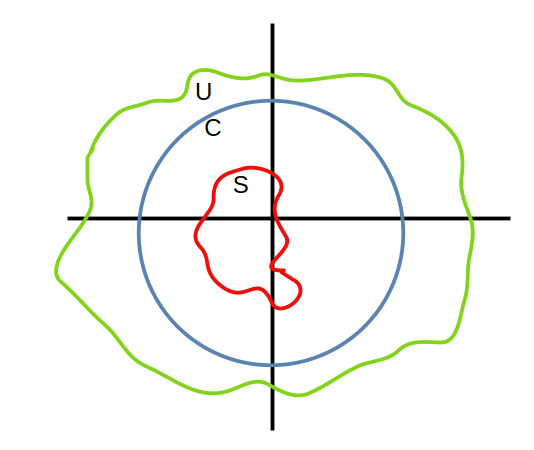
Part 1: U - this is the open set within which is analytic. It’s important that U encloses the other two sets.
Part 2: S - , the spectrum of T. It has several important properties. First, it is non-empty - this means we have to pay attention to it. It is also closed and, most importantly, bounded - being bounded means we can avoid the spectrum by being far enough away from the origin. Not important here, but the spectrum is not necessarily connected.
Part 3: C - the circular contour on which we compute the integral.
It is necessary that is completely contained within U. In this way, we can carefully choose C to be within U and away from - hence, for every point on the circular path C, is analytic and is invertible.
In this sense, we do not have a free choice of : the function to combine has to meet the constraints imposed by the spectrum of the particular operator , i.e. .
Example
As an example, I’ll use the sequence space and a diagonal operator . Chapter 2 of (Garcia, Mashreghi, and Ross 2023) describes diagonal operators, but essentially the operator is defined by a bounded set of complex numbers, , where . The spectrum of is the closure of the set of , so is bounded by .
Take as , and the function , which is analytic over all of the complex plane. For the contour to integrate over take the circle , as .
The operator can be viewed as a diagonal matrix, with terms on the leading diagonal being , and terms off the diagonal being 0. The inverse of such a matrix is again a diagonal matrix, with terms on the leading diagonal being . (Remember, is kept away from the spectrum of , so these inverses exist.)
To compute the matrix for , we compute the integral for each of the two kinds of term:
The non-diagonal terms remain as 0 as:
The terms on the leading diagonal are evaluated as:
As is entire and is within the contour circle of radius 2, Cauchy’s Integral Formula tells us:
Therefore , which is the intuitively expected result!