Introduction
One of the key ways mathematics progresses is by first identifying a pattern in a more-or-less setting, and then taking a by trying to extend this pattern to a more environment—one that is, in some sense, than the previous one. Perhaps the old pattern still holds, or perhaps it doesn’t. In the latter case, our goal is to understand exactly , in the leap of abstraction, it fails. Usually, the by-product of this process is the creation of an entirely new landscape of mathematical objects. On the one hand, these objects follow certain intuitive rules inherited from our original setting; on the other hand, they introduce fundamentally new structures. At any rate, the motto here is: as we shall explore today.
The Integers: Our First Abstraction
Our story begins with the integers (denoted here by ), which are essentially the numbers you will recite as you count the hairs on your head or the grains of sand on a beach—along with their negatives. Another way to think about them is to draw them against the backdrop of the continuum of real numbers (or simply a line, which is what the real numbers are!). They appear like a one-dimensional version of galaxies in the universe against the vacuum of space: evenly spaced and discrete, like a sieve. After all, there are integers between, say, and , whereas there are an lot of real numbers—infinite decimals—between and ! In fact, there are so many real numbers(no matter how far you zoom into the number line, you just keep seeing more) that, we cannot even them—but that is a story for another day.
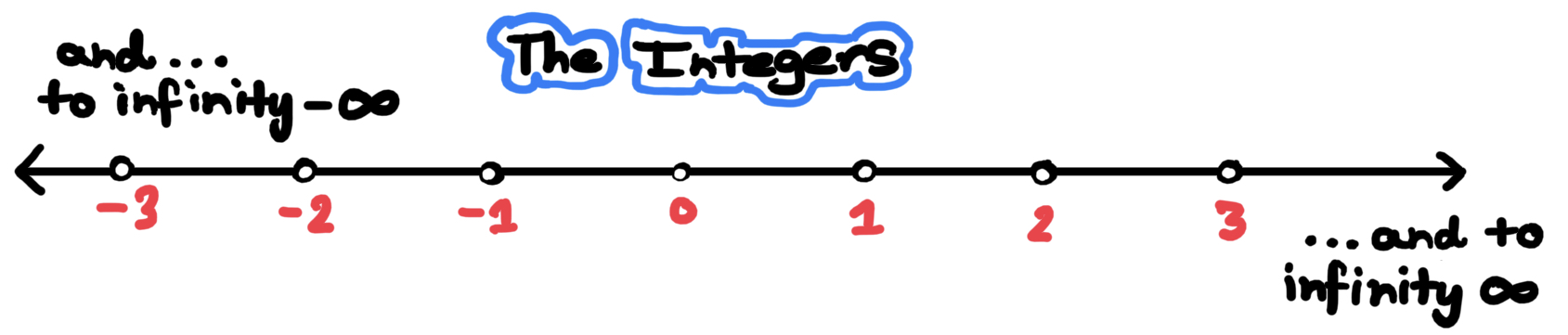
The integers aren’t terribly exciting just sitting there like dots, staring up at usand they weren’t invented to just stay put anyways! Indeed, their is to do calculationslike after measuring the length and breadth of a plot of land, say meters and meters, we would the two numbers up to get the of the plotthe number of meter by meter squares that make up the entirety of the plot. And we even developed a fool-proof to multiply to integers like and , something we learnt way back in elementary school! Notice that if I had to figure out, say, the money I would earn if I sold of my hairs for dollars each (yuck!), I would do the same thing, even though a huge amount of dirt (that is, the plot) and dead cells (that is, my hair) are nowhere near to being equal!
And just like that, we have our first, albeit , abstraction, a thing that is strewn in such high quantities across the mathematical landscape that it practically makes it up. The number is a clean ‘abstraction’, meant to represent hairs and meters of dirt at the same time! We created the integers as a whole by observing a specific commonality between two very distinct sets of objectstheir number!
The next step after getting rid of all the (In the context of counting, this was simply replacing each instance of that particular object with the same indistinguishable token, so that only differences in the number count, as opposed to a difference in structure or the appearance. At other times, we may be interested in properties of objects, so that we abstract differently, keep this in mind!) to create a set of ‘counting classes’, is to formulate meaningful rules to manipulate these ‘counting classes’. As we saw, thanks to the reasonably large degree of abstraction that went into creating the integersin that one integer can stand for a frighteningly large diversity of objectsin the first place, these rules will carry quite a bit of power.
One such rule is multiplication: On the one level, it’s just a to convert an input of two integers into a single one (one of infinitely many so called binary operationstry inventing a few yourself!), but it is deeply in a concrete physical meaningthe area of a rectangleas we saw. The other main rule is that of addition, which has a more elementary physical interpretation: the total number of objects when many collections of objects are placed side-by-side. The last step, obviously, is to interpret the result of the abstract manipulation in the context of the situation!
Taking Off
Now, we play around with the integers, building up to our central charactersa very special subset of the integers.
You might notice that given integer and the operation , you can reach positive integer: , and so on (we’re ignoring the negatives and zero for the moment), but that and keeps you stuck on . Indeed, no number and can create the whole of (the set of positive integers). Instead we must broaden our scope and ask what sub of the integers along with can generate ? Clearly we can choose , so we really should be asking for the possible . In some sense, down under multiplication as much as possible!
One way to think about this is to first our field of vision down to the set , and then increasing it to and then to , continuing on like this, just adding one number at a time, building for each of these restricted versions of . You can think about the greatest element of this chain of sets like a , and we’re pulling it out to infinity, a step at a time. We shall use denote the for .
First, for , is just the thing: you need and , as we noted above. Second, we consider . There too, you realize that you need as well, as multiplying by itself and by any number of times is , and is : so , where we added that little to denote the set of all numbers you can get by multiplying and with each other any number of times. Observe that is always contained in .
This pattern halts, at least for once, at the third set: . Here you do need to add to , as , meaning that . For the first time, we’ve been able to compress such a set, albeit to a very small degree! Try computing more ’s!
As you might’ve already guessed, is essentially the set of the so-called : the of the integers under multiplication, or the most compressed version of the integers under multiplication, as we have just seen. The other elements of (the elements of the set theoretic difference ), the numbers, are called numbers.
A playful analogy to draw here (and one that we will come back to surprisingly often) is to think of the primes as and composite numbers like from chemistry (we are not assigning primes to for a very deliberate reason!). This analogy has many limitations, one of them being that prime numbers are infinite in number, whereas there are only finitely many stable atoms, but let us overlook these transactional details for the moment.
Indeed, this connection helps us come to terms with a notable property of the integers, that of . Take the example of a molecule of wateressentially an oxygen atom stuck (the analogue of multiplication) to two hydrogen atoms. Notice that a water molecule will only ever be made up of atoms in this way: one atom connected to two atoms! Drawing on this analogy, it would seem only logical for this to hold in as well: in that every integer can be expressed as the product of primesthe composite number is and is . And, as it turns out, it does actually hold!
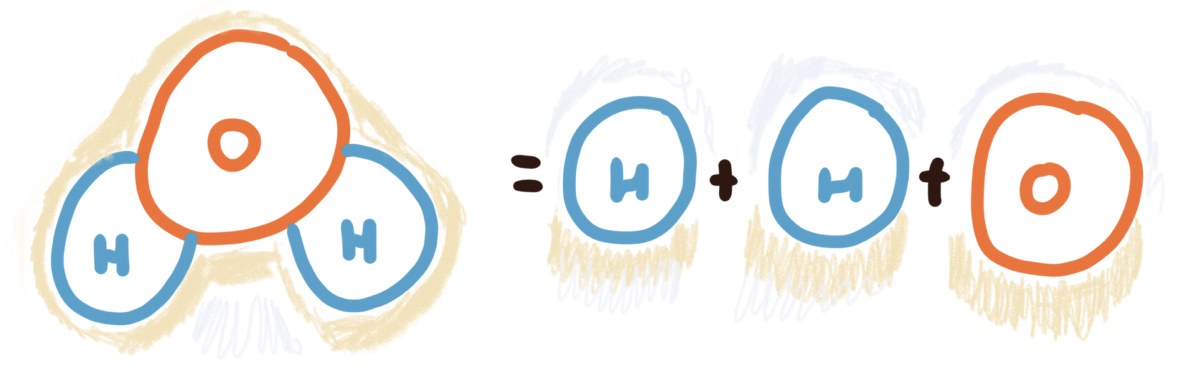
But this is not always trueonly when we are and .
What Next?
Less abstractly, we’re going to move the realm of the usual integers, creating , integer objects (mind you, there are the integers, only ), where the element has two prime factorizations! These integer like objects will live in the complex , rather than the real , as you shall soon see. Then, in an attempt to recover unique factorization in this new setting, we will find ourselves replacing individual numbers, with of numbersand so we will succeed in creating a new object as a result of to extend a broken pattern.
Before we set (pun intended!) out on our adventure to foreign landscapes, let us take one last look at divisibility in which will give a hint at those ‘sets’ we’ll ultimately be considering.
Divisibility and Sets
When we say divides (written as ) what do we ? On the one hand, it is simply saying that is an integer, as opposed to a fraction or even , a real number (formally, there exists an integer such that )but there’s also a visual way to analyse this situation.
We start with the integersevenly spaced and looking up at as usualand on them, keeping fixed, so that the distances between next-door integers increases by a factor of : is now where and is where . If we the labels on the dots and place this transformed line atop the one, we see we’re left with : the integers you’d be able to vist if you only were armed with a pair of self-regenrating arrows: one that read ‘JUMP ’ and another that read ‘JUMP ’. In fact, this a way to view the integer as : It yields the setreally a proxy of the integers, the set of all of .

Now, what happens when we place upon ? Didn’t notice? Well, try the order by placing on the base slate and placing atop that. Did you see what happend? was completely & cleanly by ! Mathematically, the set is contained in the set . This is becuase the new pairs of arrows: one created by gluing two ‘JUMP ’ arrows and the other created by gluing two ‘JUMP ’ arrows means you can visit even integers that beforeyou’ve surrendered your precise visting abilities! Essentialy this clean of sets is manifestation of the fact that try and see this!

On the other hand, the result is not satisying if we place atop or the the other way. We don’t get a clean containmentwe can see orange and red dots lurking here and there. This is preceisly becuase does divide . Indeed, is always contained in which is because every integer is divisible by .
To sum up, we can view a single integer as its version of the integers which is its multiplesand divisibility can be seen as a containment of those sets.
And now, we create our new integers.
Travelling Beyond
Let’s take another look at , this time with their space in mindthe real numbers, which is essentially a , a one dimensional object. Could we come up with an analogue of the integers for a rather than a line? That object would truly earn the moniker of a sieve.
Well, mathematically speaking, the complex numbers describe a plane, just like how the real numbers describe a line. As a review, the complex numbers is the set , which can alternatively be viewed as of real numbers, along with well-defined rules for addition, subtraction, multiplication and division. The most natural notion of an integer here would be a complex number where both the real and imaginary parts are integers: Geometrically, you’re starting with the usual integers, and translating them upwards and downwards in the complex plane by an inetger.
We’ll use to denote this notion of the complex integers (notation to be explained!). And sure enough, the picture looks pretty convincingequally spaced dots looking up at us!
What’s more is that one can add, subtract and multiply any two such elements of and get back an element of , but you necesarily divide, in the sense that the quotient of two such elements need not be in like it was in ! Try and find examples of such quotients! Recall that it was precisely becuase of the fact that you can’t cleanly divide two integers it made or to talk about divisibility (anything divides into anything in , anything divides into anything in ).
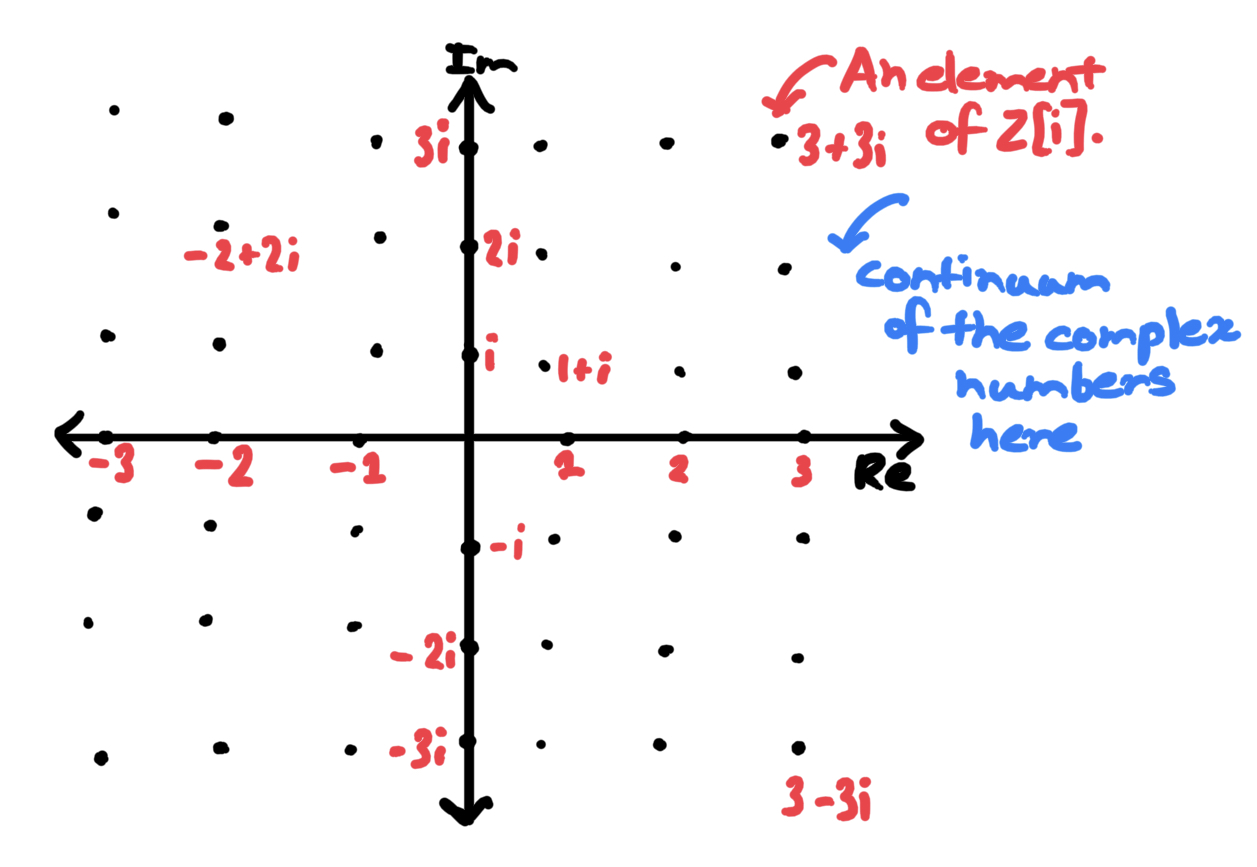
To make things seem a bit abstract, lets actually down the rules for the arithmetic operations on . How do we add and ? Just like we add complex numbers! After all, and are complex numbersjust like how adding two , say and is the as adding the numbers and . Explicitly, This sum is in because , the real part, and , the imaginary part are both integers as and are integers and an integer plus another integer is an integer! A very similar analysis can be done on the multiplication!
But this is naive thinking as well. Instead of translating the integers upwards and downwards by an , why not by an of ?
Check it out! This picture looks pretty convincing!
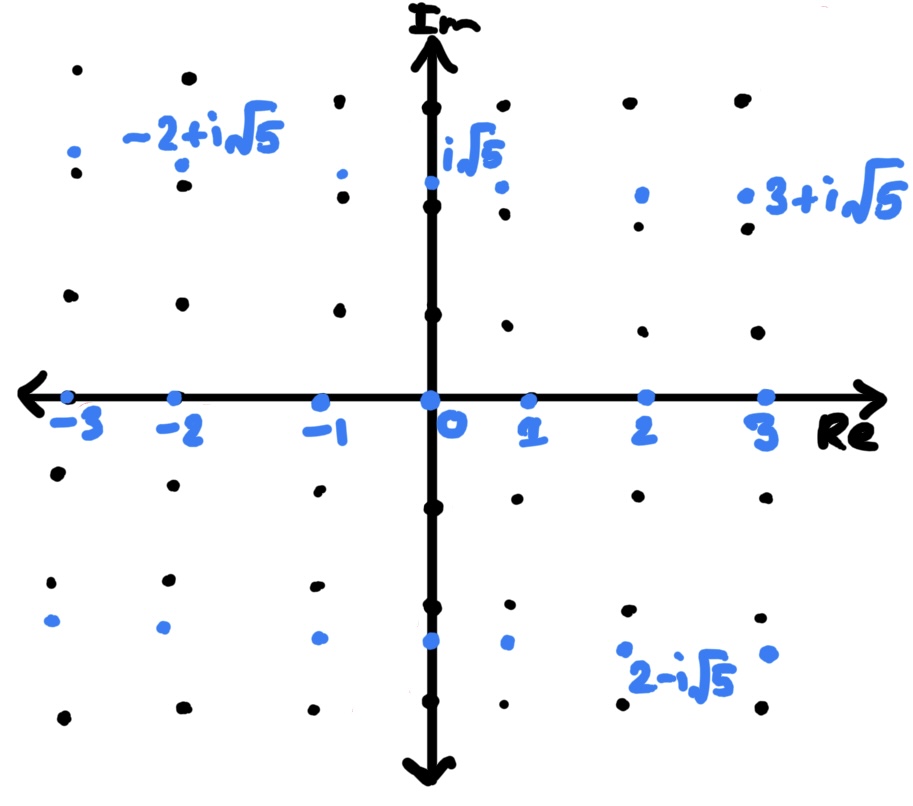
Another way to think about it is we’ve applied the transformation represented by the by matrix to each element of . We’ll denote this set by (can you geuss what the notation means?). Written down explicitly, we start with an integer , and translating it upwards/downwards by an integral multiple of is the same thing as adding for some integer (the of translation) to so . Essentially, we’ve just multiplied the vector with the matrix above.
What’s moreyou can probably geuss what’s going to happenwe can still add, subtract and multiply elements of and get back an element of try verifying this! And then, again, you can’t always divide in , so we can talk about divisibility here as well!
The astute readers among you may not be quite convincedyes, is great, but did we have to stretch in the direction ? We could have done the thing with the horizontal axis, streching it out by a factor of , say?
And we could have completely done thatthat set would still discrete (try drawing a picture), and have the basic arithmetic operations from division. The problem with that would be that we would inadverntantly the multiplicative identityin the process, and we of want that number to be around, as it was present in . Stretching in the direction allows us to keep , lying on the horizontal axis, intact.
Where are the Primes?
Before we can start doing some factorization in these new lands, as promised, we need to the notion of a prime. What does it mean for an element of or to be a prime? To answer that, we ask ?
Well, it’s a usual integer such that its only divisors are and . Phrased differently, it’s a number such that we write as a product, say where and are integers, then one of them be or . Essentially, divisors are allowed to divide that number, not even a moreand we will be using this exact definition in and .
Except that there are more trivial divisorsnumbers that divide every elementthan just and here! But what are they?
Let’s stick with first. Clearly and work, because their their multiples in is the whole of . And why is that? Because they are the to as possibletheir step size, their arrow propelles one forward as little as possible each time it is thrown. In particular, they are a distance away from the origin. Similarly, and are also a distance of from the origin, and they divide every complex number as well!
All in all, it can be shown that the four numbers are the trivial divisors! Any other number will not work because it is .
There is a way to see this algebraically as well: we are looking for such that the quotient lies in for . That is, divides all . Notice that this means that be a complex integer, simpy by setting . Conversely, has a multiplicative inverse (that is, ) in , then the quotient is in for all ! An element is a trivial divisor precisely when it is invertible!
Next, we massage the expression for a bit, by izing the denominator: Recall that both the real and imaginary parts must be integers, so that must divide and also divide . Try and see if you can complete this argument!
We can do something similar in . There, the only such numbers are the ol’ and you might be tempted by , but it is from . Indeed, is not even present in ’s version of the integers as it is to .
We call to be the of , and the units of named quite naturally! And we can define the analogue of primes in : the same definition holds for .
And now we factorize quite a benign number, to say the leastin .
The Breaking Point
Well, we all know that . But now we’re talking in , so we have more looking factorizations. In fact, notice that , and so
This might seem surprising. After all, they are many ways to write a regular integer as a productas a baby example take .
‘No way!’ you shout! How can that be? and may be irreducibles, but ? Seriously? I mean it literally comes in two parts!
But all we have to do is appeal to our freshly baked definition about irreducibleif is an irreducible, then we write for some and in , then at least one of them or be or , and if that turns out to be true, case closed!
First, let’s expand and a bit. Leveraging the set-theoretic definition of , we can write and , for integers and . Putting everything together, Now, we expand the right side, but that is likely to get . Instead, we simply take the usual complex number of both sides, We don’t want those square roots, so we simply square both sides to get Notice that both terms on the right side are integers, and the left side is obvioulsy an integerand so from an equation in involving elements in we havean equation in the integers!
Remember we want to do: show that one of or be an integer. Well, on the one hand is the product of the two integers and , and on the other hand, can be written as or as a product of two (positive) integers! So, and be one of or . Let’s go case by case!
Phew! That was some algebra heavy-lifting! But at the end of the day, look what we have is an irreducible in ! And in much the same way, it’s partner in crime, is also an irreducible. All in all, something hard to reconcile with our experince in !
And with that, we transition into resuce mode. Can we, in way, recover unique factorization in this new set-up?
Try Hard Enough and…
Kummer, a German mathematician, would have none of this corrupt, unacceptable business. The way he saw it, we ended up in such a situation simply because we hadn’t factored .
Taking this thought quite literally, his idea was to have ‘numbers’notice the quotation marks, , and such that and on the one side; and on the other side, and .
Now, on the one hand and on the other hand which would avoid all the drama! But what these mysterious characters? Surely they can’t be numberselememts of ! Indeed: Kummer merely hoped that playing around with these ’s might lead to some deeper insights.
Let’s start by focusing on . First, , so . Well, then must divide multiple of twojust like how for any . Over here, we have divides , where is in , as opposed to being in . Second, , so divides , and hence divides , where is some element of . Adding the two pieces together, divides (the sum of two multiples of is an multiple of ).
Essentially, this means that for each is ’s version of ! Or, writing it in terms of sets, where we put those funny brackets around to denote its version of the set of its multiples.
But what is the set on the left ?
Well, it is just ! Using the funny brackets, we write
After a bit of thinking, one realizes that the ought to be an : Indeed, if were any , while still remaining a version of , then it would actually be the of try seeing this yourself! That would then imply that would be a : or , but that not solve our purpose: for then would have to be , which does divide ( is not in ), meaning we don’t have a factorization at all.
All in all,
But, alas, as we already know, there is no whose version of the thing on the rightis the thing on the left. Try spelling the details out: suppose that is really in . Then use the divisibility relations that satisfies to show that it must be either or but that would mean that its version of is the whole thing, as we just discussed.
So, we must go one step , dropping the bracket: , going from a number of a set, so that
Notice that it is not just that is inside , but rather the whole of or that is inside . Recall that back in . So, we get a fleeting hint that since ,could we possibily have that the divides the ? Well, then we must find such that , which is also going to be a ! What is ?
Well, in a similar way, one reasons out that (recall that this is just the set of all possible sums of a multiple of and a multiple of in ).
But then what is What does it to multiply two sets?
We keep calm and use FOIL. More precisely, we just multiply a random element of the first set with another random element of the second set, and then do this for every pair of elements to get the product set.
Well, on the one hand, an element of the first set may be written as and an element of the second set may be written as , for some . Multiplying everything out, the product is Did you notice? Its a multiple of , since you can cleany factor out a ! And you can go the other way as well, showing that multiple of is of this form! In other words, and we have no difficulty in associating the right side with . After all, it is ! So, while is irreducible as a plain number, it is not irreducible as a version of .
We can apply the same line of reasoning to , to get that
Now, watch what happens when we multiply and you can try working through the productwe get and we also have that Along the same lines, while is irreducible as a plain number, it is not irreducible as a version of !
What has this achieved? Well, clearly and on the other side
We have recovered unique factorization! We just had to look beyond numbers and into some special sets.