Pure-Birth Processes and Pade Approximants

Consider a two-player turn-based game in which the two players take their turns at different rates and . One might ask, what is the distribution of the number of turns taken up to a given time ? We can answer this question by leveraging an interesting connection between two superficially unrelated concepts: pure-birth processes and approximations of the exponential function.

Pure-Birth Processes, Divided Differences, and Hermite-Pade Forms

A or is a particular type of continuous time Markov chain taking values in which is increasing and exclusively makes jumps of size 1. The value of the process at time is the “number of births” which have occurred by that time, and it is determined by its inter-birth times, which are independent exponentially distributed random variables. Here we will use the explicit construction of such a process described below.

A typical way to analyze a pure-birth process would be to compute its infinitesimal generator and use the Kolmogorov equations to show that its transition probabilities satisfy a certain set of recurrence relations. From there, if the inter-birth rates have some kind of regular pattern, it may be possible to use probability generating functions to get explicit formulas for the transition probabilities (see (Di Crescenzo, Iuliano, and Martinucci 2011) for a treatment like this). However, even for the simplest cases such as the two-player game described above, this method is extremely computation-heavy.

Another route is to leverage a connection between pure-birth processes and approximations of the function , utilizing the concept of divided differences. The generalized divided difference is defined recursively by


with . Notably, is symmetric in its arguments, and if , then


Generalized divided differences usually appear as the coefficients of the Hermite interpolating polynomial for a function evaluated at the arguments of the divided difference. They also have an integral representation due to Hermite and Genocchi, proved in (Atkinson 1989):

That is, the generalized divided difference of a function is given by integrating the function’s derivative over all convex combinations of its arguments. We can exploit this fact to get a general formula for the p.m.f. of any pure-birth process:

This is a remarkably nice-looking formula considering that it works for any pure-birth process, and it apparently has somehow not yet appeared in the literature. However, its aesthetic appeal is tempered by the general poor behavior of the generalized divided difference; though easy to compute recursively for any specific set of inputs, it is pretty much impossible to analyze in general. Luckily, this difficulty is mitigated in our setting by the specific properties of the exponential.

In the particular case of the exponential function, divided differences are naturally connected to the notion of Hermite-Pade approximation. Given a sequence of integers , it is a well-known result of Hermite that there exist unique (up to a constant multiple) polynomials such that each has degree at most and


where . The left hand side in the above inequality is called a (HPF) of degree and order . The most well known such form is , where and are the Pade approximant polynomials for of degrees and respectively, given by
For the function , the connection between divided differences and Hermite-Pade forms was codified by Sablonniere (Sablonnière 2003).

Application to the Two-Player Game

A special case of Theorem 3 is when , in which case we have


In Sablonniere’s paper, the result is only proved for the inputs 0 and 1 to the divided difference, and only if they each appear with multiplicity at least 1. We can rework this result for general inputs and with multiplicity , also swapping for the function .

Now, note that the two player game described in the intro is simply the pure-birth process associated with , where the turns taken are the “births” in question. The desired p.m.f. for the number of turns taken by time then falls out as a corollary of Theorems 2 and 4.

Let’s check to make sure this formula works. We can code up a simulation of the two-player game with and and get the empirical distribution for the number of turns taken up to time over 1,000,000 trials, and compare this to the plot given by our formula above:

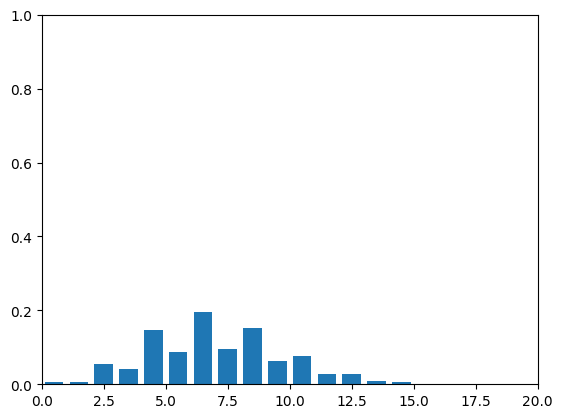
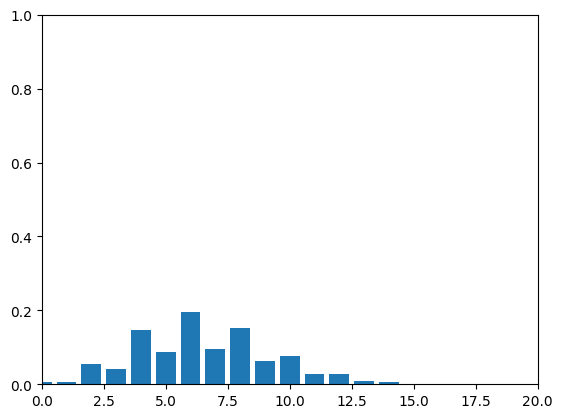
So, we’ve successfully found a formula for the p.m.f. of a pure-birth process with alternating rates. Nice! Now it just needs a catchy name; my suggestions are the “interlaced Poisson distribution” or the “dual Poisson distribution”, but I will allow the scholars of the future the freedom to decide what best to call it.

Reference