Edit: I remembered the experiment incorrectly in a first version, it’s been a while, I should have paid attention.
Few years ago, I had an internship in an optic laboratory working on metamaterials. A core tool for metamaterials is transformation optics. Transformation optics aims at finding the (ideal) optical properties of a material (electric permittivity, magnetic permeability) by means of geometric transformations. More precisely the main tool of transformation optics is to associate a space metric to the electric permittivity of a material.
That’s not the topic.
During that internship, I read an introduction to transformation optics written by Leonhardt Ulf and Thomas G. Philbin callled "Transformations optics and the geometry of light". One of the best lecture I ever had. In that introduction, the authors discuss an analog to the Aharonov Bohm effect for light. Light passing through a rotating transparent fluid behaves like electrons around an infinite coil. The light from a monochromatic source passing to the right of the "whirlpool" experiences a phase delay while the light passing to the left experiences a phase push and vice versa depending on the direction of the fluid flow. If a double slit set up is put before the whirlpool, the light passing through the two slits interfere with itself and the interference pattern is shifted by the interaction with the fluid.
The very same phenomena happens for electrons passing through two slits and then around an infinite coil, they interfere with themselves and the rotating potential vector shifts the interference pattern. The infinite coil has no electric field nor magnetic field outside of the coil. There is a magnetic flow inside the coil.
It’s all very interesting and a typical quantum phenomenon. In classical physics, charges only interact through forces, and only the electric and magnetic field are considered "real" (by who? good question). Potentials, on the opposite, can be transformed with a gauge transformation, and thus, it is impossible to measure them. You can only measure differences of potentials, and differences of potentials usually lead to forces. In the Aharonov Bohm effect, the opposite is true, electric and magnetic field are not measurable, and you can only measure the phase delay between two wave fronts circulating along different potentials (namely the vector potential).
The circulation of the vector potential can be related to the magnetic flow traversing a section of the coil , which is an integral version of the relation . Which means it can be related to a classical field, but the interaction is non local, or the wavefunction transforms locally, but it interacts with a "non physical" field, the vector potential. If the phase of the wavefunction changes locally, then, there is a good chance that the momentum changes too. That relation itself is allowed by the Maxwell equation . So historically, the vector potential is a mathematical artefact, a tool, not an observation, it is therefore funny to find afterwards phenomenon that could only be explained by the vector potential. The funny bit in it is the non locality of the relation . And since the flow of the magnetic field, out of a real coil, should be opposite to the one inside the coil, we also have the relation .
That is the first point that bothered me a lot with that effect. How forces can be the real stuff in classical physics while in quantum mechanics potentials are more relevant?
Another point hitching a bit is that, at the time I was reading the paper, there was no definitive proof that the electric analog of the AB effect was real. The AB effect happens when someone considers an electric charge passing through a vector potential . The electrical Aharonov Bohm effect is an analoguous effect but for the scalar potential . And there can not be any variation of the scalar potential without an electric field. At the time, lots of experiments had been performed, all of them observed the effect, but...There was always an artefact force explaining it coming from an electric field created by that very same potential which was supposed to create the effect. This had me thinking, since the electric potential can be transferred to the vector potential through a gauge choice and vice versa, maybe..., just maybe, there is an electric field explaining the usual good old Aharonov Bohm effect.
Third point worth being noticed is that very few papers are interested by the interaction between the coil and the electron. Even when considering the vector potential as the source of the effect, the electron itself is also a source of a vector potential. That potential should have an effect (at least) on the charges in the coil, and maybe on the wave itself, but this becomes way too speculative. Its electric field and its magnetic field should have an effect too. There are papers discussing the effect. (references to be put)
Fourth point is that a single charge circulating around a circular path radiates, and thus it loses speed. In consequence, it does not create the same vector potential after one loop around a circle. For a single charge, you would have to push it continuously to maintain its speed, one way to do so is to add... a scalar potential. In a real, non supraconductive, coil, the Joule effect dissipates the energy electrons acquired and you always need to compensate for the loss of energy by maintaining a steady scalar potential, this translates into a charge accumulation.
You can see the link between the two potentials by using the Lorenz gauge and the fact that it is a 4 potential.
where is a Lorentz scalar but it can be a function of space and time
So if is constant ( BIG IF ) there is an electric field created by a scalar gradient each time there is a gradient of the norm of the vector potential, and the intensity of it is governed by the ratio .
Interestingly when a very small gradient of the vector potential gives rise to an electric field. BUT, on the other side, the narrow minded physicist will yell because is a bit meaningless. The scalar potential can be defined up to a constant term! We said that we were in Lorenz gauge, and then, the scalar potential is uniquely defined by the potential created by adding all potentials created by localised single charges with a zero potential at infinity.
There are mathematical proofs that a closed circuit does not radiate, mostly because all radiations compensate each other, although I am not sure how accurate that statement is in real life with wires where discrete charges circulate, and how charges circulating in different parts of the circuit manage to absorb all the radiations emitted by the others.
In a real loop, to maintain a steady current, there would be the need for a scalar potential, so for a half loop, on side of the loop is always at a higher potential than the other.
Finally I thought that a single charge circulating around a circle at great speed would be like a half oscillation of a radiating source going away and a half oscillation of a radiating source coming.
So with all those points, I put myself in the desperate quest of an electric field that would mimic the classical Aharonov Bohm effect if charges were "classical". I searched for an electric field proportional to .
An electric field proportionnal to that value would have the perfect properties, it would be irrotational and from the simulation I ran, a charge passing through that field would just be deviated without gaining or losing momentum. The reason for that is that at infinity any charge deviated also passes on the opposite side (picture to be put).
Now that I am once again raving about it, I realise that a sort of fairly localised electron beam, like a gaussian beam, passing only (or mostly) on one side of the coil should experience a phase shift only in one direction. Could it be assimilated to an acceleration?
Besides
From there we can say that two situations are equivalent. The first is there is no electric field nor any scalar potential gradient and so
the second is that there is an electric field entierely created by the scalar gradient and once again
So what we have to evaluate is . If it’s proportional to
then you can discard any pair
or
or
The choice of discarding the second one would result in
The problem is that so even if this is not equal, a rotating electric field would not be noticed, and the scalar product is always equal to zero. So it has to be that
Let’s see if we can extract the effect of an electric field on the path in a different way. In the paper Asymmetry of the Aharonov-Bohm diffraction pattern and Ehrenfest’s theorem, the authors prove that the Ehrenfest theorem is verified and that . They then deduce that the electron experiences no force. I missread the paper, it uses an odd notation. Usually, the canonical momentum is denoted while the momentum of the electron is noted the authors do the opposite. So it seems there is no net force on the charge, so no electric field.
STILL. I know that I am usually extremely rigorous (lol), but let’s
be loose here. It is possible to find such a field. Let’s take the coil
created by a real wire. Real wires are not neutral, everybody thinks
they are, but they are not. Real wires are resistive, and therefore they
demonstrate a voltage between two different points of the wire when a
steady current flow through them. 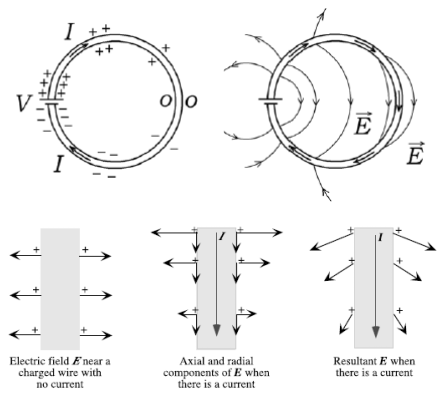
Source: a question on https://electronics.stackexchange.com/questions/532541/is-the-electric-field-in-a-wire-constant quoting (Sources: top - Andre Koch Torres Assis, Julio Akashi Hernandes, "The Electric Force of a Current", bottom - "Understanding Electricity and Circuits: What the Text Books Don’t Tell You", Ian M. Sefton)
So let’s take a charged conductor loop with a total charge . According to some French artificial intelligence, (which I will trust here), the field created by that loop in the loop plan is radial and its expression is
With a complicated value of that needs no further explanations.
Now let’s imagine that the charge is actually not constant, and that it changes when an observer rotates around the charged loop. Let’s imagine it changes linearly.
If the total charge was the electric field would be
The difference of electric field between the two is
This is where I am super loose, I should write the electric field coming from a small portion of a wire, with a linear density of charges instead of a total charge, but let’s be cowboys. It can thus be written.
And so when ,
and
Let’s forget about that loose and silly calculation. The Lorenz gauge provides a formula for the vector potential:
And because in a real wire,
we have:
So when , there is little need for a gradient, but what happens then just before the resistance drops to 0? Is there a quantized resistivity?
So the next step is just to simulate the effect of an electric field created by a real wire and compare it to a pure vector potential.
Note that the formula also provides a link to the scalar potentials created by individual charges:
Ok enough for raving about that idea for now, it belongs to the ugly category, but I like it a lot, I am not done with it.
To be continued... when and if I ever have time to do so.