These notes are intended to form part of a series on things I’ve learned or discovered about the Smith aperiodic monotile, and more generally about edge substitutions of polygonal tilings with edge-matching conditions. Up till now I’ve been posting on Mastodon and The Tiling List (a mailing list for tiling enthusiasts), and I have a few documents on Google Drive, but I’d like to have a coherent exposition in one place that’s publicly accessible and supports longer expositions.
At some stage I may expand this post to cover other parallels between the Fibonacci tiling and the Hat aperiodic monotile, but at the moment I just consider the question whether the ‘lifted’ tiles can be approximated by a line in or .
Define the substitution to be the group endomorphism1 on the free group on two elements, and , determined by We can define related endomorphisms on the set of right-infinite, left-infinite, and bi-infinite words on the alphabet , using the limit of acting on finite approximations. We’ll continue to use for these endomorphisms.
Here we will only consider words with letters that have positive exponents, but for the Hat tiling, we will need to consider inverses, so we set things up in this context, even though it isn’t necessary.
For a bi-infinite sequence of ’s and ’s, we use a dot to indicate the point in the sequence between the numbers at positions and , for example The deflation of such a sequence is . For example, the deflation of the sequence is We then say that is the inflation of .
The -shift operator moves a sequence steps to the right, so for example A sequence is a Fibonacci sequence if it is some shift of the deflation of another Fibonacci sequence, in other words, if there exist bi-infinite sequences and shifts such that and for all . Note that we can restrict to lie in the set .
Each bi-infinite sequence of ’s and ’s has a geometric representation as a tiling of the real line, using a prototile set with two tiles which are both unit intervals, and where the dot corresponds to . An alternative geometric representation can be given by ‘lifting’ it to a staircase in , where the -tiles correspond to horizontal segments of unit length, the -tiles correspond to vertical segments of unit length, and the dot corresponds to .
Note that the end-point of the lift of a finite word is the image of under the abelianisation map that sends to and to . If is the abelianisation of , we have a commutative diagram so if we draw the image of the lift of a word under multiplication by , it will coincide with the lift of for all prefixes of . We can see this in figure 1 , where the grey paths on the right are the images under multiplication by of the lifted words to the left. Here denotes the lift of a word, and the grey dot denotes the origin. Segments have been decorated with arrows, which aren’t necessary here, but are included for consistency with figure 3.
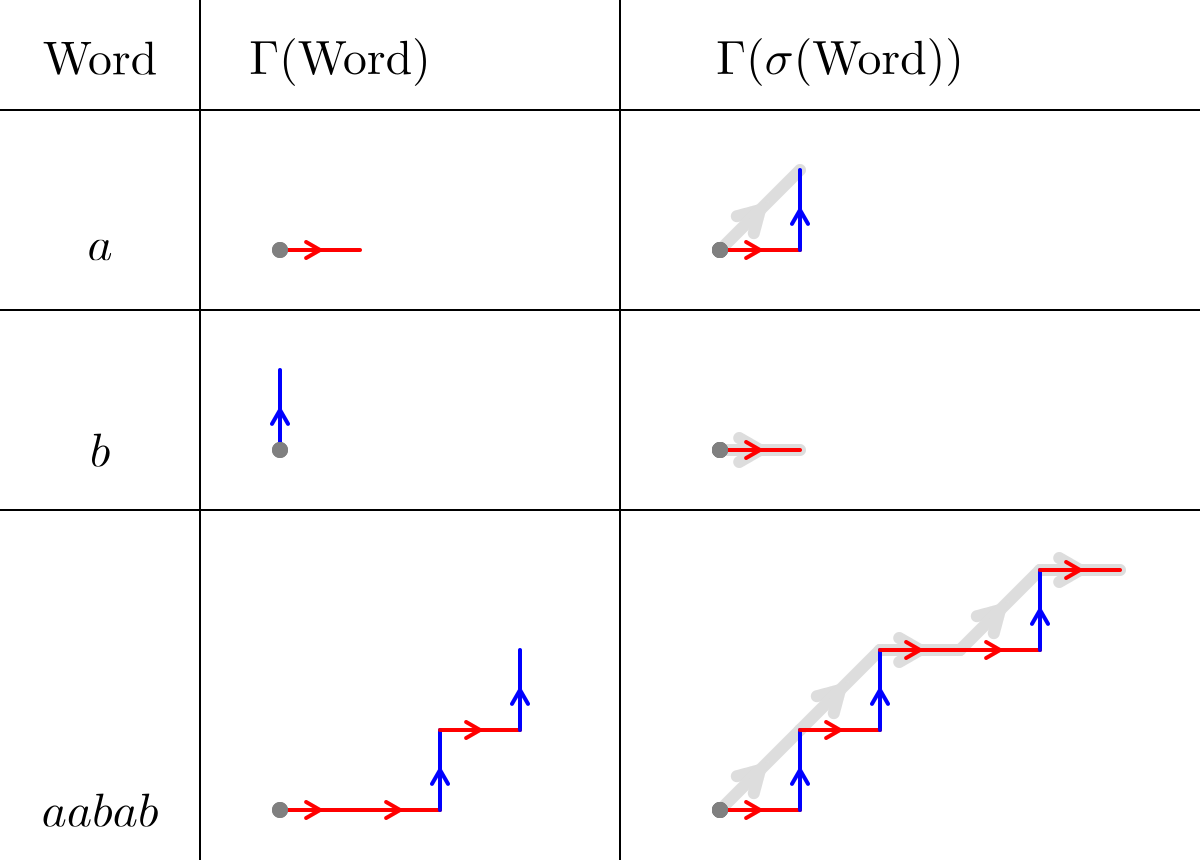
The tiling of the line associated to a Fibonacci sequence is then equivalent to the orthogonal projection of the associated staircase onto the line , up to rescaling. More generally, for , the orthogonal projection of the staircase onto the line is equivalent to a tiling of the line by two tiles which are intervals whose lengths are in proportion .
Let be the set of vertices of a lifted Fibonacci tiling. By definition, this is the shift of the deflation of another Fibonacci tiling, so the set of vertices of the lift of this tiling satisfies for some offset . For example:
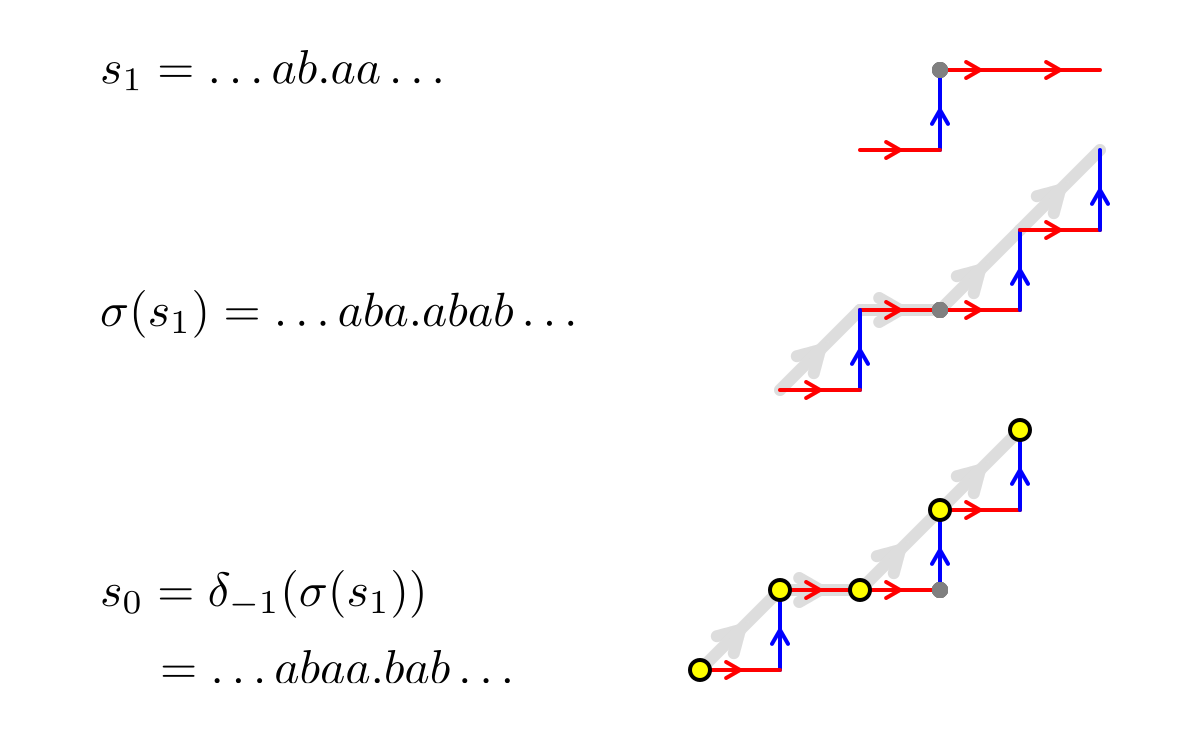
In the bottom row of figure 2 , the vertices are shown as yellow dots. A vertex will either be contained in or differ from it by . Either way, for some , so for some and .
By iterating this process, for all we can find and in the set of vertices of lifts of Fibonacci tilings with By induction, for any ,
Let and be the eigenvalues of that have moduli respectively greater and less than 1, and let and be the projections from onto the respective eigenspaces, which we denote and - the expanding and contracting spaces. Thus for all , If we apply to (), we get so Since , as the term approaches , while the sum on the right remains bounded by a convergent geometric series. Thus there is (independent of ) such that eventually remains in the ball of radius about the origin.
This will be proved below, so for now we assume it is true and proceed with the rest of the proof.
Suppose has been chosen large enough so that for all , lies in a ball of radius . By the claim, lies in a ball of radius , for some depending only on .
Now apply to () to get Since and are bounded and , we can take the limit to deduce that which is bounded by where .
Returning to claim , note that since the tiles have length at least and at most , the ball of radius around the origin can intersect at most tiles in any tiling, so any vertex can be joined to the origin in by a path of length at most , and thus is bounded by .
This may seem like a strange way to prove the claim, which follows more directly by noting that the projection of the staircase onto is a tiling with finite local complexity, but we make the argument above since a modification of it will be needed in the case of the Hat tiling.
In fact, we can construct a situation involving the Fibonacci tiling that requires a similar modification. Fix , and define which up to rescaling is the orthogonal projection onto the line . Suppose we wanted to prove claim in this context.
Let be the set of left endpoints of lifted tiles, ordered by the order of the tiles in the sequence, and for , let be those endpoints with . Since Fibonacci sequences don’t contain adjacent ’s, consecutive elements in differ by the vector or . Therefore the displacement between the -projections of such points is either or . In either case the displacement is positive, so the size of is bounded by , and each vertex in is not more than steps away from the origin.
Each vertex in the staircase is at most one step from a vertex in , so if , then it is not more than steps away from the origin, where is the length of the projection of the lift of . These bounds can certainly be improved, but we just care about their existence. This completes the proof of the claim in this case.
By a ‘Hat’ tiling, we refer to a family of tilings described by Smith et al., which contain tilings by ‘chevron’, ‘turtle’, ‘hat’ and ‘comet’ tiles, among infinitely many others. Our point of view is that these are just different projections of a single object - the lift of the tilings.
We will work with the comet-rhomb version of the Hat tiling, a tiling by three polygonal prototiles with coloured edges that must match. This is described in work by Arnaud Chéritat (implicitly), mathBlock and James Smith.
Instead of working with the free group on two letters, we work with the free group on twelve letters which correspond to directed edges of the tiles, or equivalently, to directions in the lifting space.
Let be the cyclic group of order 6; in this context the most natural way to represent it is as the 6th roots of unity: Since acts on by (subscripts taken modulo 6), it acts on and its abelianisation, which we can identify with the additive group of .
The analogue of the Fibonacci substitution is the -equivariant homomorphism defined by
Figure 3 shows the result of applying to the rhomb and even and odd comets. Note that this is intended to represent the -lifts of the tiles, but to draw them we need to chose some (arbitrary) projection to . The one chosen here corresponds to a tile halfway between the hat and spectre versions.
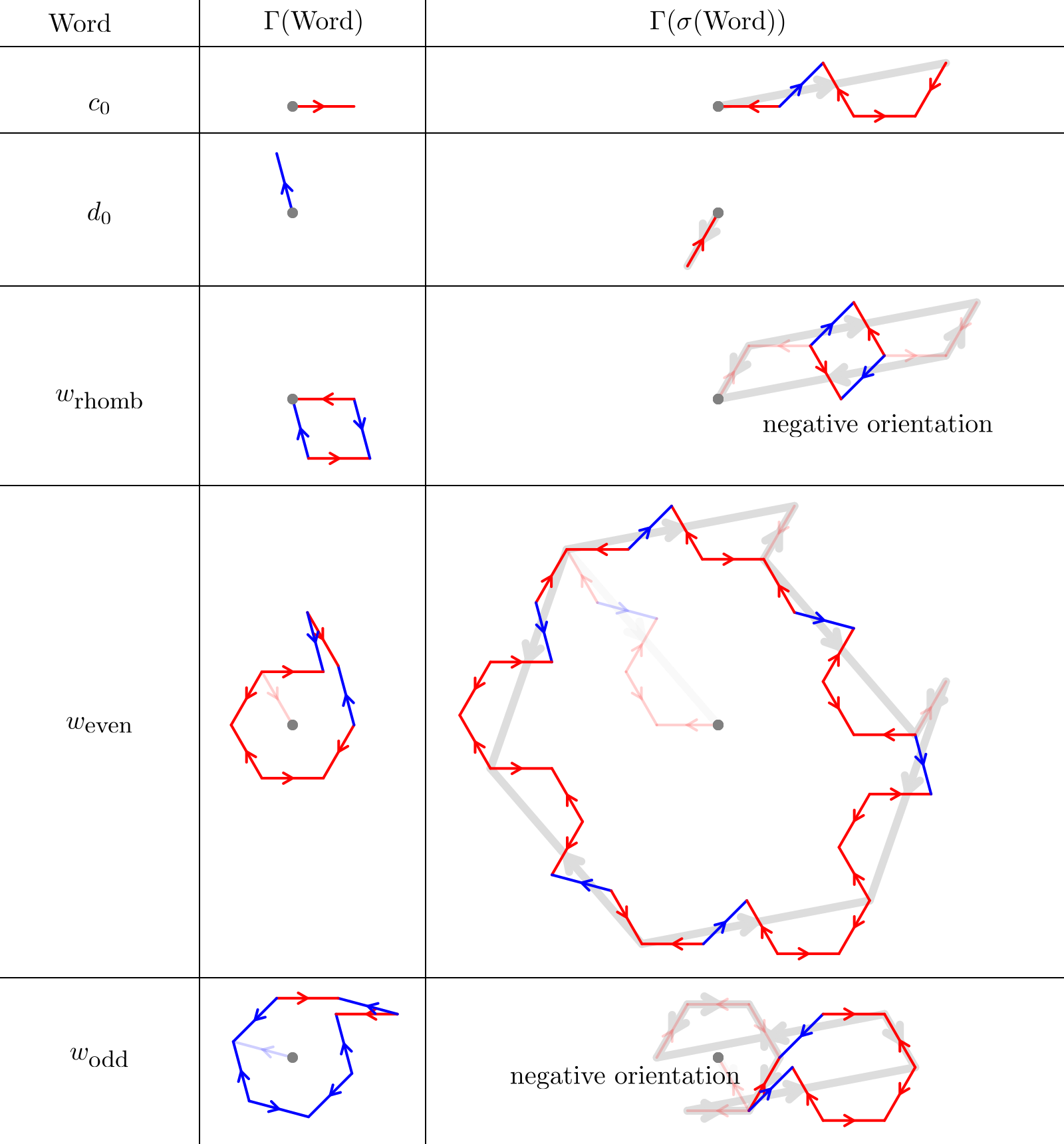
If and correspond to the lifted points and in respectively, then the analogue of the transformation matrix used for the Fibonacci tiling is the matrix Figure 4 shows the vertices (shown in yellow), for the vertices of an even tile, and the decomposition of the transformed shape into an patch.
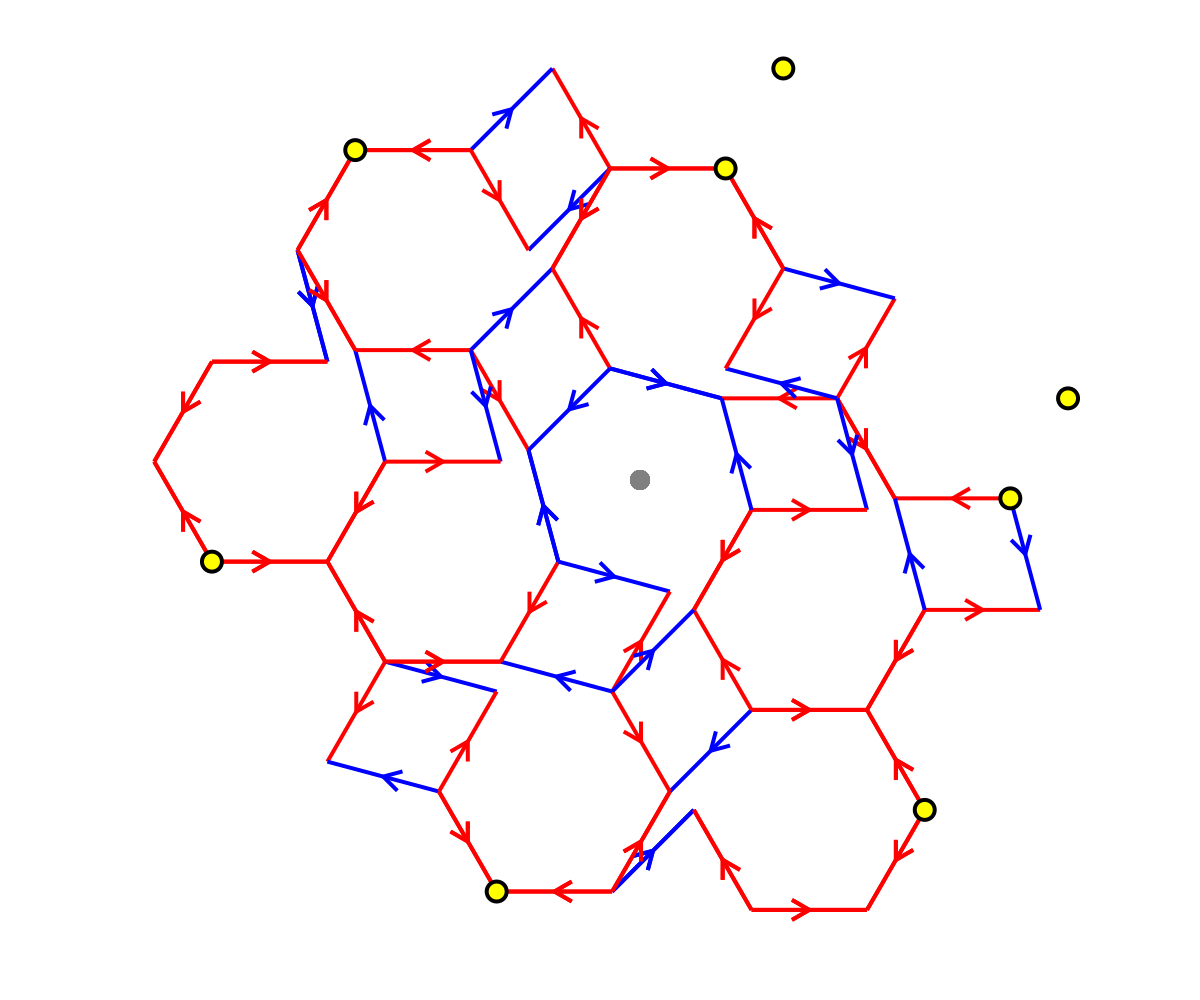
Each vertex in the deflated patch differs from some vertex in by an offset coming from a finite set , so we are in the same situation as the Fibonacci tiling. The proof proceeds as before, with the following differences:
and .
is replaced by , so the eigenspaces are complex lines.
The vertices lie in the product of two copies of the Eisenstein integers instead of .
The proof of claim in this context needs to be modified.
Regarding the last point, we will consider the -projections of the centres of lifted even2 comet tiles, as an analogue of the left endpoints of lifted -tiles in the Fibonacci tiling.
Consider paths between centres of even tiles in the lift that consist of moving along straight lines between adjacent points in . By considering cases, each pair of adjacent even tile centres has a connecting path that is some rotation by a power of of the ones shown below3. Here we show the word associated to each path, as well as its image under the abelianisation map (which gives the coordinate of the end of the path in ).
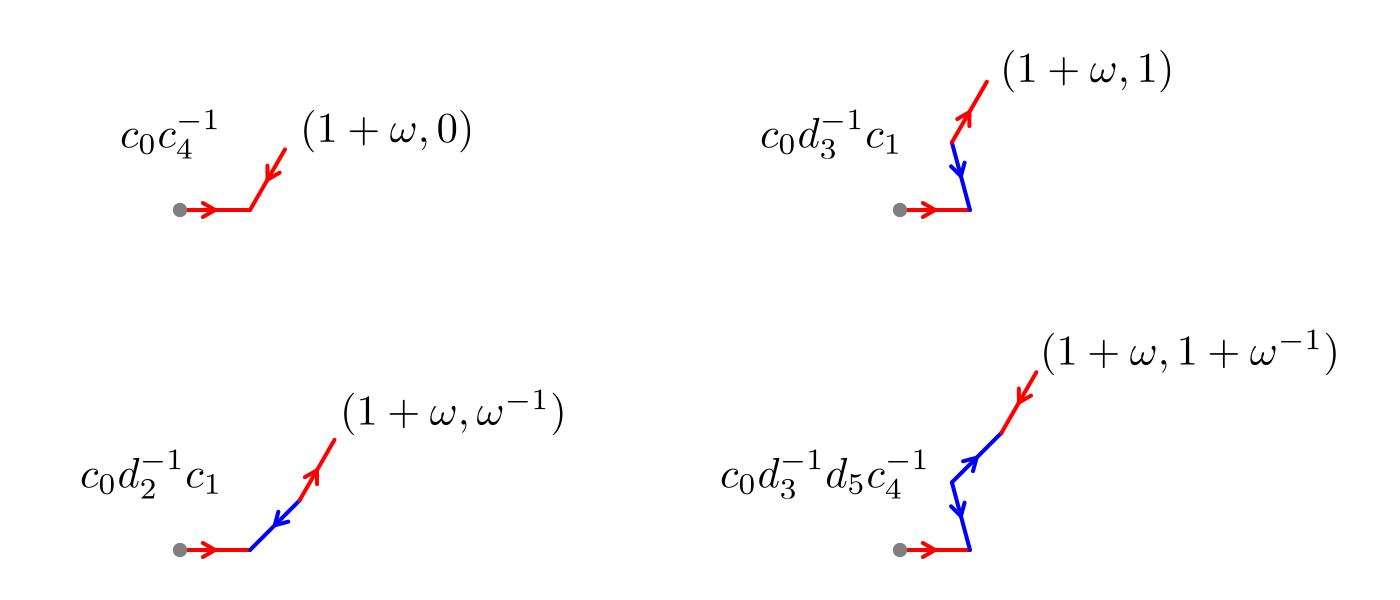
Therefore the displacements between adjacent even centres in are all of the form up to multiplication by powers of . Thus the modulus of the second coordinate is at most .
If we project from onto using the map the even tiles in the lifted tiling are mapped to tiles of a hexagonal tiling, so their centres form a triangular grid. The projection , up to rescaling, is which we can think of as a perturbation of the projection onto the first coordinate, since is smallish. In figure 6 we show various projections4 of a lifted patch of tiles:
Left: the projection giving rise to a conventional tiling in the Hat family (the same as in figure 3 ),
Centre: the projection under ,
Right: the projection under .
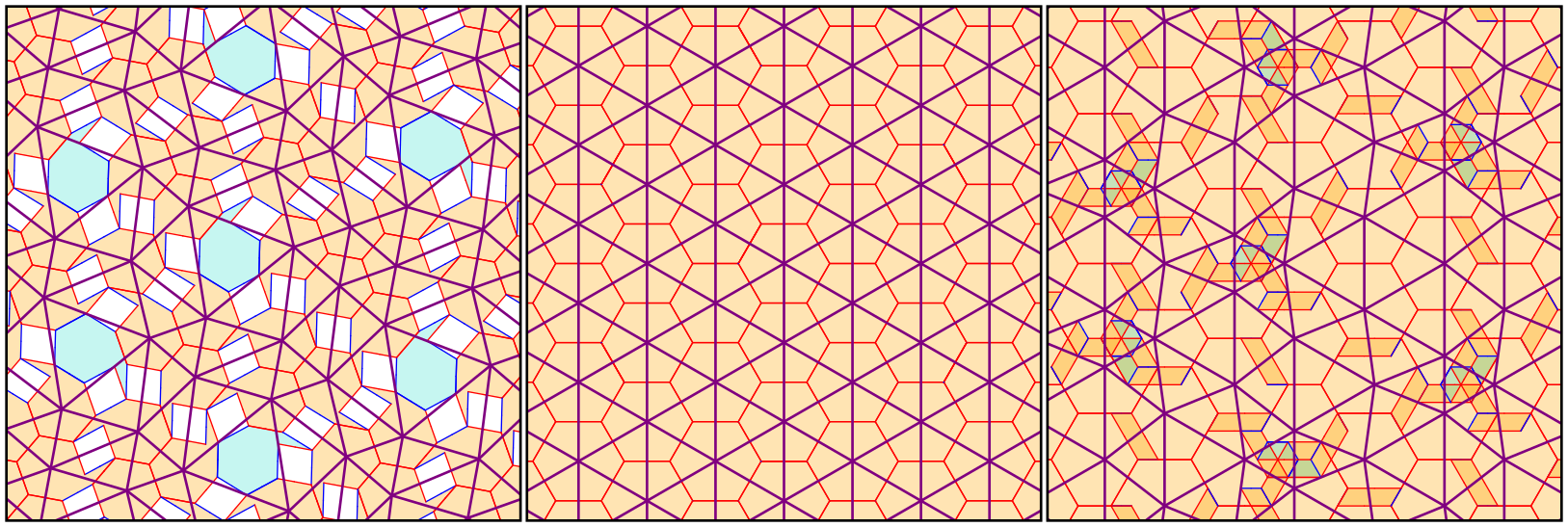
The purple segments join centres of adjacent even tiles, and as observed above, form a regular triangular grid in the case of . To show that they still lie on a (deformed) triangular grid for the perturbed projection , consider the triangle in formed by three mutually adjacent vertices, where the tiling has been translated so that one of them is at the origin.
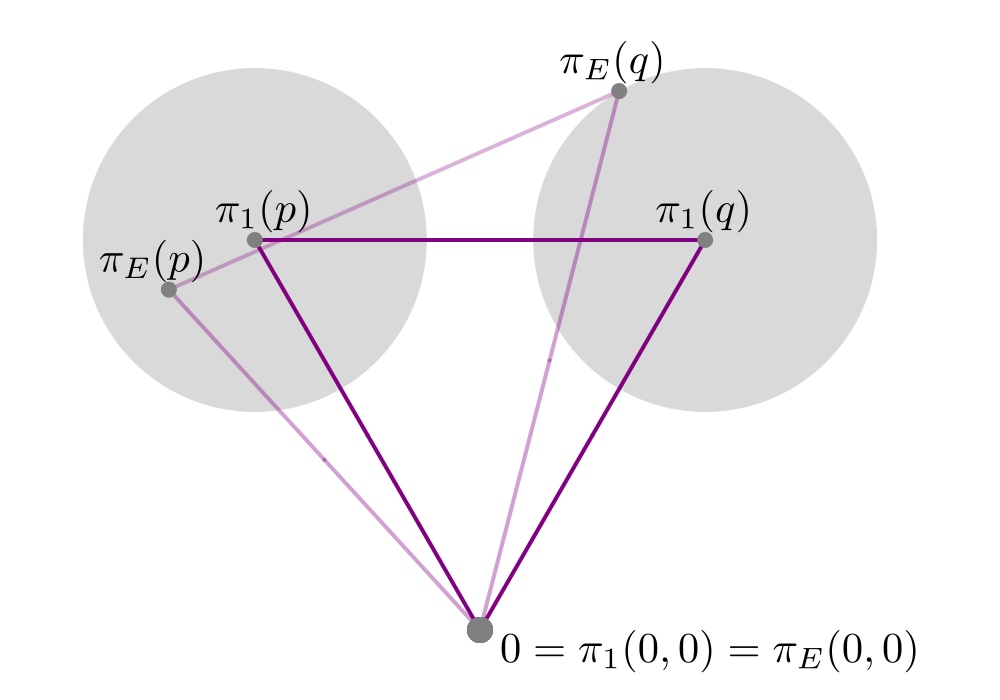
Figure 7 shows the projection of this triangle onto under and . From , the equilateral triangle has edges of length , while the perturbed projections of vertices ( and ) have moved a distance of at most (the radius of the grey circles) from and respectively. Since , these circles are disjoint, so none of the triangles can flip orientation, and thus the tiling of the plane by triangles whose vertices lie on even tile centres remains a conventional tiling.
Let be the minimum area of these triangles. If we subdivide each triangle into three polygons of equal area, we can associate to each even tile centre a neighbourhood of area at least , where neighbourhoods associated to different odd tile centres only overlap on their boundaries.
Consider all the even tile centres in a ball of radius . If is the maximum diameter of a triangle, the ball can contain at most even tile centres, since the ball of radius contains all the neighbourhoods of the even tile centres. This completes the central part of the claim, and the rest proceeds as in the proof of the Fibonacci tiling projected onto , .
